Question Number 138384 by mohammad17 last updated on 13/Apr/21

$${find}\:{the}\:{singular}\:{point}\: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\frac{{e}^{{z}} }{{z}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\frac{{sin}\left({z}\right)}{{z}} \\ $$$$ \\ $$$${help}\:{me}\:{sir} \\ $$
Answered by Mathspace last updated on 13/Apr/21
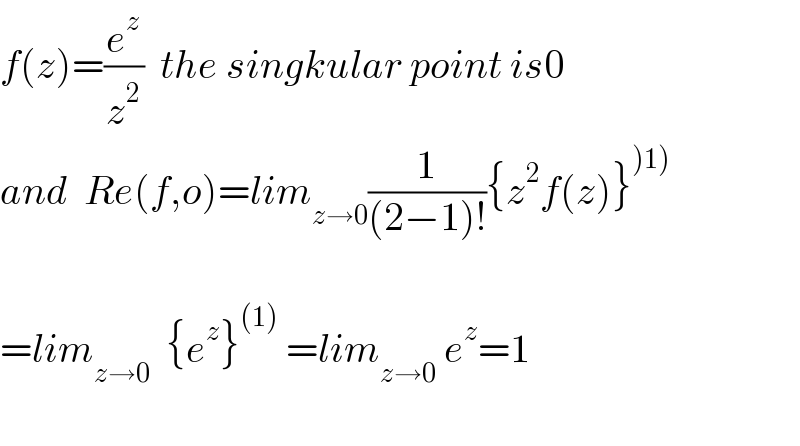
$${f}\left({z}\right)=\frac{{e}^{{z}} }{{z}^{\mathrm{2}} }\:\:{the}\:{singkular}\:{point}\:{is}\mathrm{0} \\ $$$${and}\:\:{Re}\left({f},{o}\right)={lim}_{{z}\rightarrow\mathrm{0}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{{z}^{\mathrm{2}} {f}\left({z}\right)\right\}^{\left.\right)\left.\mathrm{1}\right)} \\ $$$$ \\ $$$$={lim}_{{z}\rightarrow\mathrm{0}} \:\:\left\{{e}^{{z}} \right\}^{\left(\mathrm{1}\right)} \:={lim}_{{z}\rightarrow\mathrm{0}} \:{e}^{{z}} =\mathrm{1} \\ $$$$ \\ $$
