Question Number 1077 by Vishal last updated on 07/Jun/15
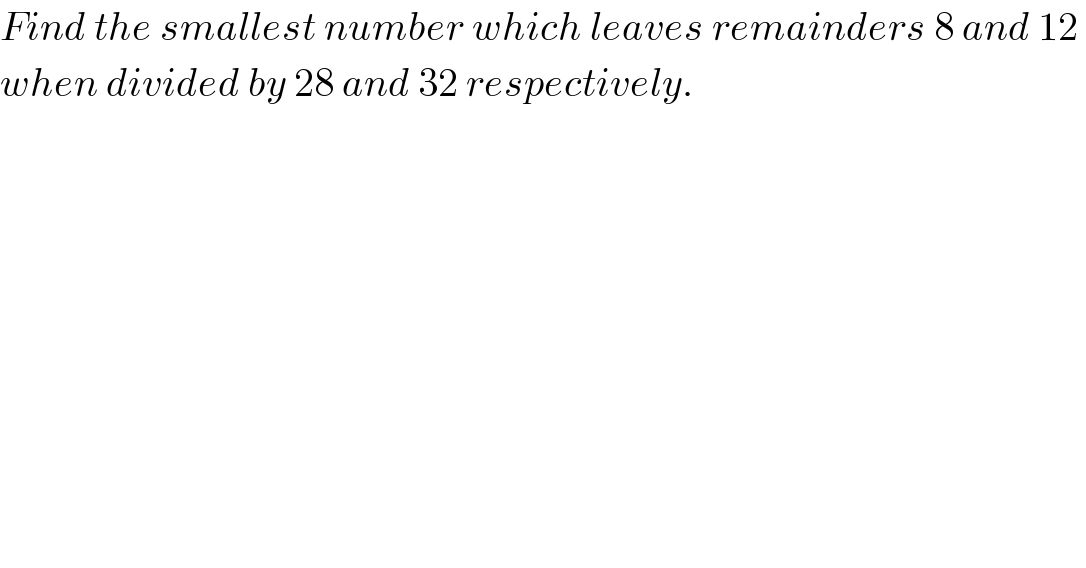
$${Find}\:{the}\:{smallest}\:{number}\:{which}\:{leaves}\:{remainders}\:\mathrm{8}\:{and}\:\mathrm{12}\: \\ $$$${when}\:{divided}\:{by}\:\mathrm{28}\:{and}\:\mathrm{32}\:{respectively}. \\ $$
Commented by prakash jain last updated on 07/Jun/15
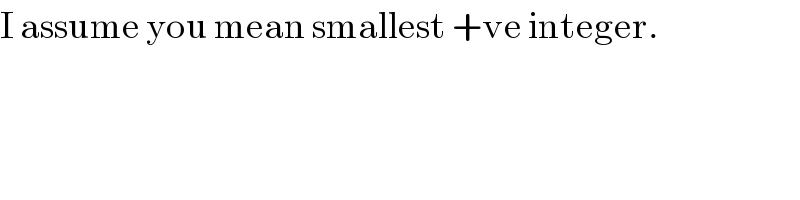
$$\mathrm{I}\:\mathrm{assume}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{smallest}\:+\mathrm{ve}\:\mathrm{integer}. \\ $$
Answered by prakash jain last updated on 07/Jun/15
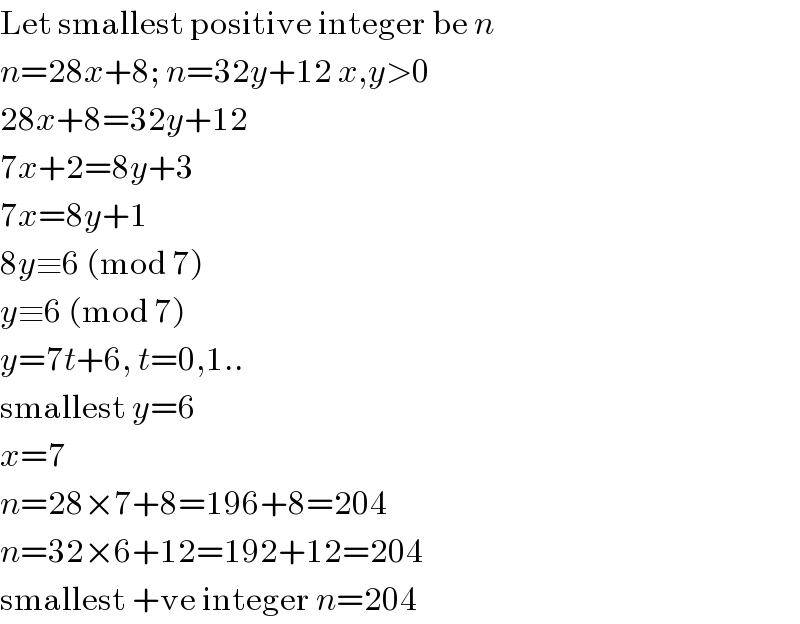
$$\mathrm{Let}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{be}\:{n} \\ $$$${n}=\mathrm{28}{x}+\mathrm{8};\:{n}=\mathrm{32}{y}+\mathrm{12}\:{x},{y}>\mathrm{0} \\ $$$$\mathrm{28}{x}+\mathrm{8}=\mathrm{32}{y}+\mathrm{12} \\ $$$$\mathrm{7}{x}+\mathrm{2}=\mathrm{8}{y}+\mathrm{3} \\ $$$$\mathrm{7}{x}=\mathrm{8}{y}+\mathrm{1} \\ $$$$\mathrm{8}{y}\equiv\mathrm{6}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$${y}\equiv\mathrm{6}\:\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$$${y}=\mathrm{7}{t}+\mathrm{6},\:{t}=\mathrm{0},\mathrm{1}.. \\ $$$$\mathrm{smallest}\:{y}=\mathrm{6} \\ $$$${x}=\mathrm{7} \\ $$$${n}=\mathrm{28}×\mathrm{7}+\mathrm{8}=\mathrm{196}+\mathrm{8}=\mathrm{204} \\ $$$${n}=\mathrm{32}×\mathrm{6}+\mathrm{12}=\mathrm{192}+\mathrm{12}=\mathrm{204} \\ $$$$\mathrm{smallest}\:+\mathrm{ve}\:\mathrm{integer}\:{n}=\mathrm{204} \\ $$
