Question Number 6086 by sanusihammed last updated on 12/Jun/16
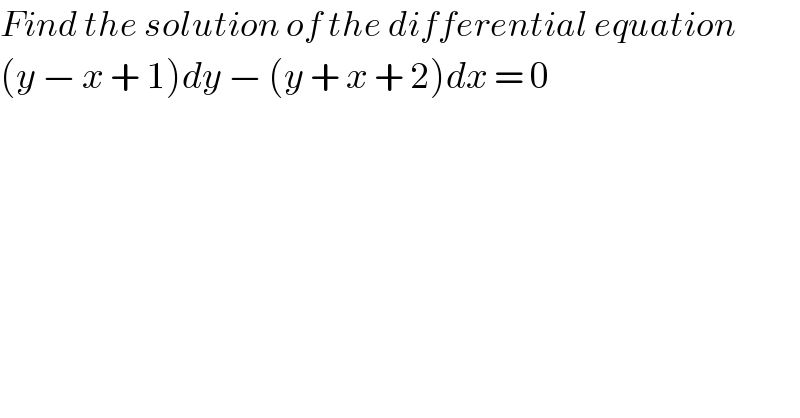
$${Find}\:{the}\:{solution}\:{of}\:{the}\:{differential}\:{equation}\: \\ $$$$\left({y}\:−\:{x}\:+\:\mathrm{1}\right){dy}\:−\:\left({y}\:+\:{x}\:+\:\mathrm{2}\right){dx}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by Yozzii last updated on 12/Jun/16

$${M}\left({x},{y}\right){dx}+{N}\left({x},{y}\right){dy}=\mathrm{0} \\ $$$${M}\left({x},{y}\right)=−{y}−{x}−\mathrm{2}\:,\:{N}\left({x},{y}\right)={y}−{x}+\mathrm{1} \\ $$$$\frac{\partial{M}\left({x},{y}\right)}{\partial{y}}=−\mathrm{1}\:,\:\frac{\partial{N}\left({x},{y}\right)}{\partial{x}}=−\mathrm{1} \\ $$$$\therefore\:\frac{\partial{M}\left({x},{y}\right)}{\partial{y}}=\frac{\partial{N}\left({x},{y}\right)}{\partial{x}}\:\Rightarrow\:{the}\:{given} \\ $$$${differential}\:{equation}\:{is}\:{exact}. \\ $$$$\Rightarrow\exists{g}\left({x},{y}\right)\in\mathbb{R}\:{such}\:{that}\:\frac{\partial{g}\left({x},{y}\right)}{\partial{x}}={M}\left({x},{y}\right), \\ $$$$\frac{\partial{g}\left({x},{y}\right)}{\partial{y}}={N}\left({x},{y}\right)\:{and}\:{d}\left({g}\left({x},{y}\right)\right)={M}\left({x},{y}\right){dx}+{N}\left({x},{y}\right){dy}. \\ $$$$\frac{\partial{g}}{\partial{x}}=−{y}−{x}−\mathrm{2}\Rightarrow{g}=\int\left(−{y}−{x}−\mathrm{2}\right){dx} \\ $$$${g}\left({x},{y}\right)=−{xy}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}+{h}\left({y}\right)…..\left({i}\right) \\ $$$$ \\ $$$${Also},\:\frac{\partial{g}}{\partial{y}}={y}−{x}+\mathrm{1}\Rightarrow{g}=\int\left({y}−{x}+\mathrm{1}\right){dy} \\ $$$${g}\left({x},{y}\right)=\frac{{y}^{\mathrm{2}} }{\mathrm{2}}−{xy}+{y}+{f}\left({x}\right)…..\left({ii}\right) \\ $$$${Comparing}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{suggests}\:{that} \\ $$$${g}\left({x},{y}\right)=−{xy}+\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+{y}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}+{D} \\ $$$${with}\:{the}\:{possibility}\:{of}\:{an}\:{added}\:{constant}\:{D}. \\ $$$${Now}\:{since}\:{M}\left({x},{y}\right){dx}+{N}\left({x},{y}\right){dy}=\mathrm{0} \\ $$$$\Rightarrow{d}\left({g}\left({x},{y}\right)\right)=\mathrm{0}\Rightarrow{g}\left({x},{y}\right)=\int\mathrm{0}{dx}={C} \\ $$$$\Rightarrow{y}−\mathrm{2}{x}−{xy}+\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+{D}={C} \\ $$$${or}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{4}{x}−\mathrm{2}{xy}+{E}=\mathrm{0}. \\ $$$${This}\:{is}\:{an}\:{implicit}\:{solution}. \\ $$$$ \\ $$
Commented by sanusihammed last updated on 13/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
