Question Number 143846 by mathmax by abdo last updated on 18/Jun/21
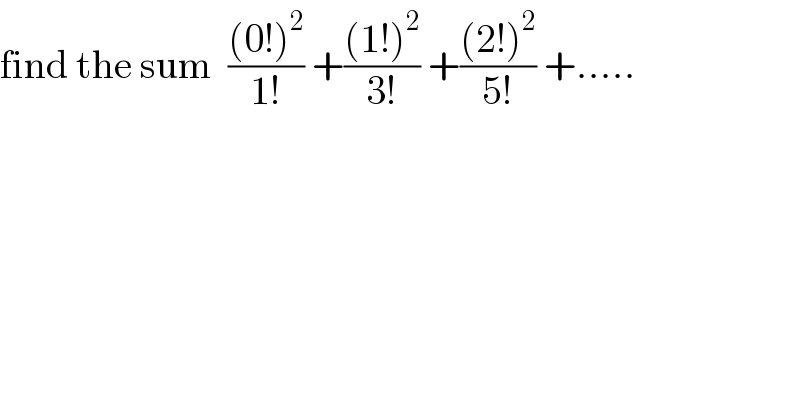
$$\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\:\frac{\left(\mathrm{0}!\right)^{\mathrm{2}} }{\mathrm{1}!}\:+\frac{\left(\mathrm{1}!\right)^{\mathrm{2}} }{\mathrm{3}!}\:+\frac{\left(\mathrm{2}!\right)^{\mathrm{2}} }{\mathrm{5}!}\:+….. \\ $$
Answered by Ar Brandon last updated on 18/Jun/21
![(((n!)(n!))/((n+n+1)!))=((Γ(n+1)Γ(n+1))/(Γ(2n+2)))=β(n+1, n+1) S=(((0!)^2 )/(1!)) +(((1!)^2 )/(3!)) +(((2!)^2 )/(5!)) +∙∙∙=Σ_(n=0) ^∞ β(n+1,n+1) =∫_0 ^1 Σ_(n=0) ^∞ x^n (1−x)^n =∫_0 ^1 (1/(1−(x−x^2 )))dx =∫_0 ^1 (dx/(x^2 −x+1))=∫_0 ^1 (dx/((x−(1/2))^2 +(3/4))) =[(2/( (√3)))arctan(((2x−1)/( (√3))))]_0 ^1 =(2/( (√3)))((π/6)+(π/6))=((2(√3)π)/9)](https://www.tinkutara.com/question/Q143854.png)
$$\frac{\left(\mathrm{n}!\right)\left(\mathrm{n}!\right)}{\left(\mathrm{n}+\mathrm{n}+\mathrm{1}\right)!}=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{2n}+\mathrm{2}\right)}=\beta\left(\mathrm{n}+\mathrm{1},\:\mathrm{n}+\mathrm{1}\right) \\ $$$$\mathrm{S}=\frac{\left(\mathrm{0}!\right)^{\mathrm{2}} }{\mathrm{1}!}\:+\frac{\left(\mathrm{1}!\right)^{\mathrm{2}} }{\mathrm{3}!}\:+\frac{\left(\mathrm{2}!\right)^{\mathrm{2}} }{\mathrm{5}!}\:+\centerdot\centerdot\centerdot=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\beta\left(\mathrm{n}+\mathrm{1},\mathrm{n}+\mathrm{1}\right) \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{x}−\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:\:=\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi}{\mathrm{9}} \\ $$
Commented by mathmax by abdo last updated on 19/Jun/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$
Commented by Ar Brandon last updated on 19/Jun/21
$$\mathrm{Your}\:\mathrm{welcome},\:\mathrm{Sir}. \\ $$
