Find-the-sum-r-0-n-3r-5-n-r-5-n-0-8-n-1-11-n-2-3n-5-n-n-as-a-simple-function-of-n-

Question Number 519 by Yugi last updated on 25/Jan/15

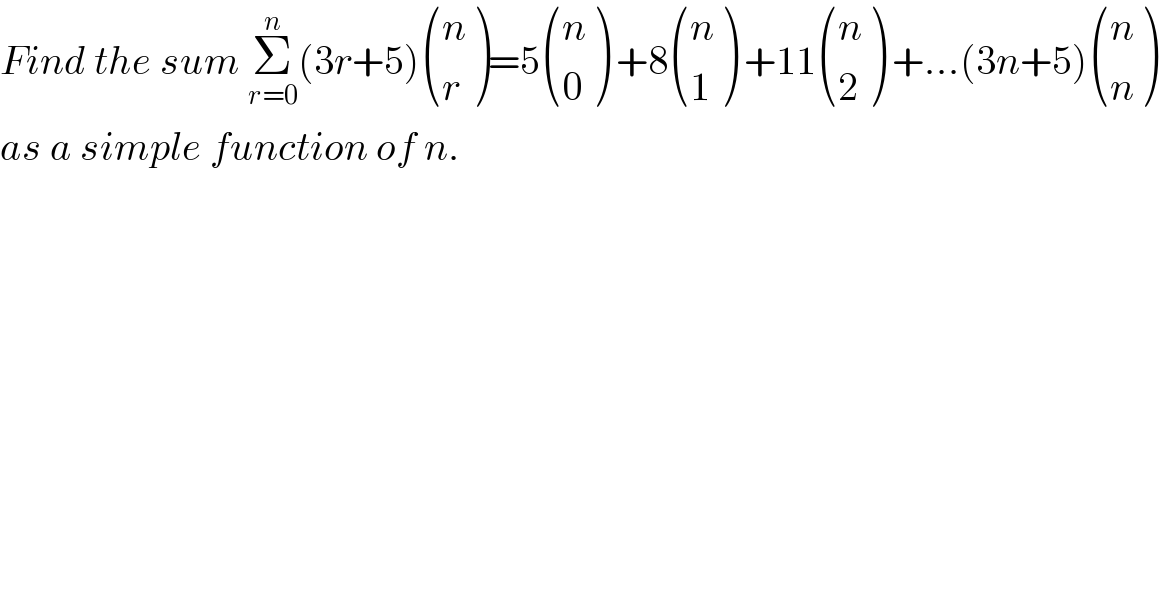
F i n d t h e s u m \underset{r = 0}{\sum^{n}} (3 r + 5) (\begin{matrix} n \\ r \end{matrix}) = 5 (\begin{matrix} n \\ 0 \end{matrix}) + 8 (\begin{matrix} n \\ 1 \end{matrix}) + 11 (\begin{matrix} n \\ 2 \end{matrix}) + \dots (3 n + 5) (\begin{matrix} n \\ n \end{matrix})

a s a s i m p l e f u n c t i o n o f n .

Commented by prakash jain last updated on 22/Jan/15

\underset{r = 0}{\sum^{n}} (3 r + 5)^{n} C_{r}

Answered by prakash jain last updated on 23/Jan/15

\underset{r = 0}{\sum^{n}} (3 r + 5)^{n} C_{r} = 3 \underset{r = 0}{\sum^{n}} r^{n} C_{r} + 5 \underset{r = 0}{\sum^{n}}^{n} C_{r}

= 3 n \cdot 2^{n - 1} + 5 \cdot 2^{n}

N o t e

2^{n} = {(1 + 1)}^{n} =^{n} C_{0} +^{n} C_{1} + \dots +^{n} C_{n}

\underset{r = 0}{\sum^{n}} r^{n} C_{r} =^{n} C_{1} + 2^{n} C_{2} + \dots . + n^{n} C_{n}

= n + 2 \frac{n (n - 1)}{1 \cdot 2} + 3 \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} + \dots + n \cdot \frac{n (n - 1) . . 1}{1 \cdot 2 \cdot \dots \cdot n}

= n [1 + \frac{(n - 1)}{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} + \dots + \frac{(n - 1) (n - 2) \dots 1}{1 \cdot 2 \cdot \dots (n - 1)}]

= n [^{n - 1} C_{0} +^{n - 1} C_{1} +^{n - 1} C_{2} + \dots +^{n - 1} C_{n - 1}]

= n \cdot 2^{n - 1}

Commented by 112358 last updated on 23/Jan/15

T h a n k s a l o t

Facebook Tweet Pin