Question Number 2207 by Yozzi last updated on 08/Nov/15
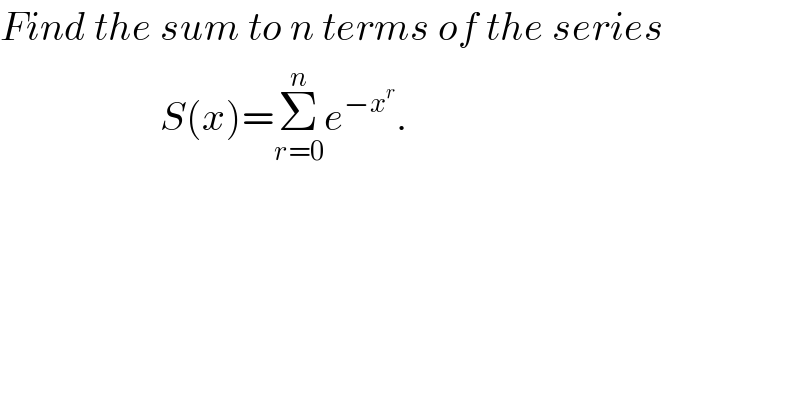
$${Find}\:{the}\:{sum}\:{to}\:{n}\:{terms}\:{of}\:{the}\:{series} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{S}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{−{x}^{{r}} } . \\ $$
Commented by 123456 last updated on 09/Nov/15
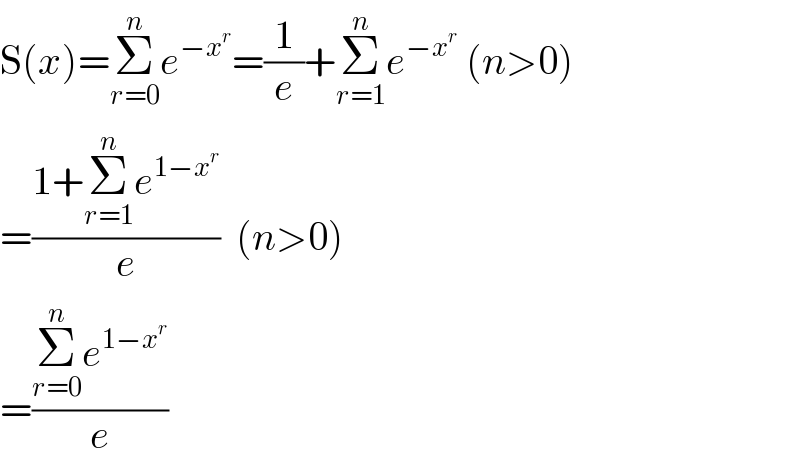
$$\mathrm{S}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{−{x}^{{r}} } =\frac{\mathrm{1}}{{e}}+\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{−{x}^{{r}} } \:\left({n}>\mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}+\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\mathrm{1}−{x}^{{r}} } }{{e}}\:\:\left({n}>\mathrm{0}\right) \\ $$$$=\frac{\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{\mathrm{1}−{x}^{{r}} } }{{e}} \\ $$
Answered by Rasheed Soomro last updated on 16/Nov/15
![S(x)=Σ_(r=0) ^n e^(−x^r ) e^x =1+x+(x^2 /(2!))+(x^3 /(3!))+...+(x^n /(n!)) −−−−−−−−−−−−−−−−−−−−−−−−−−−−− e^(−x^0 ) =e^(−1) =1−1+(1/(2!))−(1/(3!))+...±(1/(n!)) [+ for even n, − for odd n] +e^(−x^1 ) =e^(−x) =1−x+(x^2 /(2!))−(x^3 /(3!))+...±(x^n /(n!)) +e^(−x^2 ) = =1−x^2 +(x^4 /(2!))−(x^6 /(3!))+...±(x^(2n) /(n!)) +e^(−x^3 ) = =1−x^3 +(x^6 /(2!))−(x^9 /(3!))+....±(x^(3n) /(n!)) +e^(−x^4 ) = =1−x^4 +(x^8 /(2!))−(x^(12) /(3!))+...±(x^(4n) /(n!)) +.... .... ..... .... ..... ....... +.... .... ...... .... ..... ....... +e^(−x^n ) S(x) is sum of n+1 geometric series S(x)=(1+1+...n+1 terms)−(1+x+x^2 +...n+1 terms) +(1/(2!))(1+x^2 +x^4 +...n+1 terms)−(1/(3!))(1+x^3 +x^6 +...n+1 terms) ...+(1/(n!))(1±x^n +x^(2n) ....n+1 terms) [+for even n, −for odd] =1(n+1)−((1(1−x^(n+1) ))/(1−x))+(1/(2!))(((1(1−(x^2 )^(n+1) )/(1−x^2 ))).... =(n+1)−(((1−x^(n+1) ))/(1−x))+(1/(2!))(((1−(x^2 )^(n+1) )/(1−x^2 )))−... Continue](https://www.tinkutara.com/question/Q2288.png)
$${S}\left({x}\right)=\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{−{x}^{{r}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…+\frac{{x}^{{n}} }{{n}!} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\:\:\:\:{e}^{−{x}^{\mathrm{0}} } ={e}^{−\mathrm{1}} =\mathrm{1}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+…\pm\frac{\mathrm{1}}{{n}!}\:\:\:\left[+\:{for}\:{even}\:{n},\:−\:{for}\:{odd}\:{n}\right] \\ $$$$+{e}^{−{x}^{\mathrm{1}} } ={e}^{−{x}} =\mathrm{1}−{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…\pm\frac{{x}^{{n}} }{{n}!} \\ $$$$+{e}^{−{x}^{\mathrm{2}} } =\:\:\:\:\:\:\:=\mathrm{1}−{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{3}!}+…\pm\frac{{x}^{\mathrm{2}{n}} }{{n}!} \\ $$$$+{e}^{−{x}^{\mathrm{3}} } =\:\:\:\:\:\:\:=\mathrm{1}−{x}^{\mathrm{3}} +\frac{{x}^{\mathrm{6}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{9}} }{\mathrm{3}!}+….\pm\frac{{x}^{\mathrm{3}{n}} }{{n}!} \\ $$$$+{e}^{−{x}^{\mathrm{4}} } =\:\:\:\:\:\:\:=\mathrm{1}−{x}^{\mathrm{4}} +\frac{{x}^{\mathrm{8}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{12}} }{\mathrm{3}!}+…\pm\frac{{x}^{\mathrm{4}{n}} }{{n}!} \\ $$$$+….\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\:\:\:\:\:…..\:\:\:\:\:….\:\:\:\:…..\:\:\:……. \\ $$$$+….\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\:\:\:\:\:\:……\:\:\:\:….\:\:\:…..\:\:\:……. \\ $$$$+{e}^{−{x}^{{n}} } \\ $$$${S}\left({x}\right)\:\:\:{is}\:\:\:{sum}\:{of}\:{n}+\mathrm{1}\:\:{geometric}\:{series} \\ $$$${S}\left({x}\right)=\left(\mathrm{1}+\mathrm{1}+…{n}+\mathrm{1}\:{terms}\right)−\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…{n}+\mathrm{1}\:{terms}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}!}\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} +…{n}+\mathrm{1}\:{terms}\right)−\frac{\mathrm{1}}{\mathrm{3}!}\left(\mathrm{1}+{x}^{\mathrm{3}} +{x}^{\mathrm{6}} +…{n}+\mathrm{1}\:{terms}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…+\frac{\mathrm{1}}{{n}!}\left(\mathrm{1}\pm{x}^{{n}} +{x}^{\mathrm{2}{n}} ….{n}+\mathrm{1}\:{terms}\right)\:\:\left[+{for}\:{even}\:{n},\:−{for}\:{odd}\right] \\ $$$$\:\:\:\:=\mathrm{1}\left({n}+\mathrm{1}\right)−\frac{\mathrm{1}\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{\mathrm{2}!}\left(\frac{\mathrm{1}\left(\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} \right.}{\mathrm{1}−{x}^{\mathrm{2}} }\right)…. \\ $$$$\:\:\:=\left({n}+\mathrm{1}\right)−\frac{\left(\mathrm{1}−{x}^{{n}+\mathrm{1}} \right)}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{\mathrm{2}!}\left(\frac{\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−{x}^{\mathrm{2}} }\right)−… \\ $$$${Continue} \\ $$
