Menu Close

Find-the-times-in-a-day-when-the-hour-s-minute-s-and-second-s-hand-of-a-clock-occupy-the-same-angular-position-old-question-reposted-

Tinku Tara 0 Comments
Pin




Question Number 67208 by mr W last updated on 24/Aug/19
Find the times in a day when the hour′s, minute′s and second′s hand of a clock occupy the same angular position. [old question reposted]
$${Find}\:{the}\:{times}\:{in}\:{a}\:{day}\:{when} \\ $$$${the}\:{hour}'{s},\:{minute}'{s}\:{and}\:{second}'{s} \\ $$$${hand}\:{of}\:{a}\:{clock}\:{occupy}\:{the}\:{same} \\ $$$${angular}\:{position}. \\ $$$$\left[{old}\:{question}\:{reposted}\right] \\ $$
Commented by Kunal12588 last updated on 24/Aug/19
at 12 am and 12 pm?
Commented by mr W last updated on 24/Aug/19
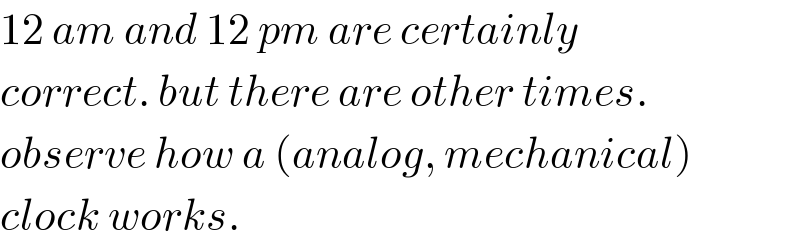
12 am and 12 pm are certainly correct. but there are other times. observe how a (analog, mechanical) clock works.
$$\mathrm{12}\:{am}\:{and}\:\mathrm{12}\:{pm}\:{are}\:{certainly} \\ $$$${correct}.\:{but}\:{there}\:{are}\:{other}\:{times}. \\ $$$${observe}\:{how}\:{a}\:\left({analog},\:{mechanical}\right) \\ $$$${clock}\:{works}. \\ $$
Commented by Tinkutara@ last updated on 24/Aug/19
22 times like 1:05,2:10,3:15,4:20,.... ?
$$\mathrm{22}\:{times}\:{like}\:\mathrm{1}:\mathrm{05},\mathrm{2}:\mathrm{10},\mathrm{3}:\mathrm{15},\mathrm{4}:\mathrm{20},…. \\ $$$$? \\ $$
Commented by Kunal12588 last updated on 24/Aug/19
at those times hour′s hand and minute′s hands have same angular position but second′s hand has differnt angular position. isn′t it.
$${at}\:{those}\:{times}\:{hour}'{s}\:{hand}\:{and}\:{minute}'{s}\:{hands} \\ $$$${have}\:{same}\:{angular}\:{position}\:{but}\:{second}'{s}\:{hand} \\ $$$${has}\:{differnt}\:{angular}\:{position}.\:{isn}'{t}\:{it}. \\ $$
Commented by mr W last updated on 24/Aug/19
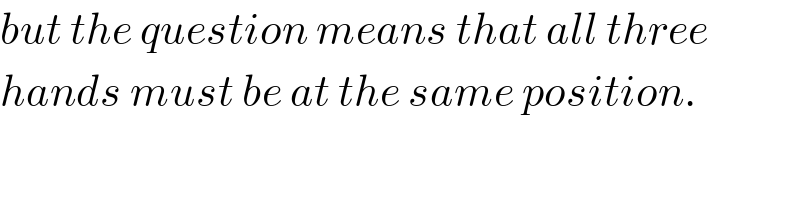
but the question means that all three hands must be at the same position.
$${but}\:{the}\:{question}\:{means}\:{that}\:{all}\:{three} \\ $$$${hands}\:{must}\:{be}\:{at}\:{the}\:{same}\:{position}. \\ $$
Commented by behi83417@gmail.com last updated on 24/Aug/19
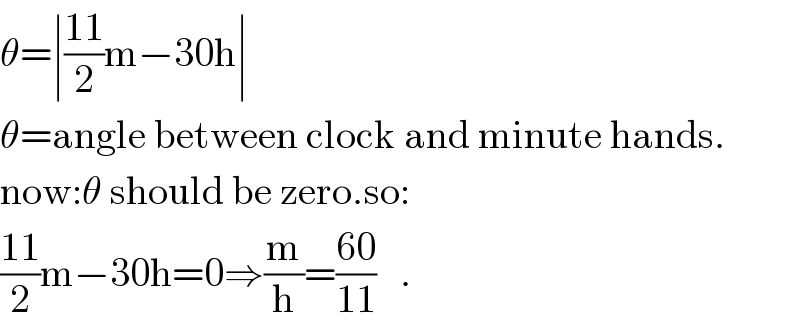
θ=∣((11)/2)m−30h∣ θ=angle between clock and minute hands. now:θ should be zero.so: ((11)/2)m−30h=0⇒(m/h)=((60)/(11)) .
$$\theta=\mid\frac{\mathrm{11}}{\mathrm{2}}\mathrm{m}−\mathrm{30h}\mid \\ $$$$\theta=\mathrm{angle}\:\mathrm{between}\:\mathrm{clock}\:\mathrm{and}\:\mathrm{minute}\:\mathrm{hands}. \\ $$$$\mathrm{now}:\theta\:\mathrm{should}\:\mathrm{be}\:\mathrm{zero}.\mathrm{so}: \\ $$$$\frac{\mathrm{11}}{\mathrm{2}}\mathrm{m}−\mathrm{30h}=\mathrm{0}\Rightarrow\frac{\mathrm{m}}{\mathrm{h}}=\frac{\mathrm{60}}{\mathrm{11}}\:\:\:. \\ $$
Answered by mr W last updated on 25/Aug/19
Commented by mr W last updated on 25/Aug/19
this picture shows an analog clock. its hands don′t move continuously, but can only occupy 60 possible angular positions: 0,1,2,...,58,59 the hands move in following way: the second′s hand moves a step every second. the minute′s hand doesn′t move with each move of the second′s hand. only after 60 steps of the second′s hand (i.e. after 60 seconds) the minute′s hand moves a step, and so on. similarly the hour′s hand doesn′t move with each move of the minute′s hand. only after 12 steps of the minute′s hand (i.e. after 12 minutes or 720 seconds) the hour′s hand moves a step, and so on. with this knowledge about how the hands of a clock work, we can determine the moments when the three hands of a clock are at the same angular position. let′s say the time is h o′clock exactly. (0≤h≤11). at this moment the hour′s hand is at the position 5h, and the minute′s and second′s hands are at position 0. after x seconds, with 0<x<3600, the position of the second′s hand is mod(x,60). the position of the minute′s hand is ⌊(x/(60))⌋, the position of the hour′s is 5h+⌊(x/(720))⌋. such that the three hands are at the same position: 5h+⌊(x/(720))⌋=⌊(x/(60))⌋=mod(x,60) we get following results: for h=0: x=0 ⇒time 0h0m0s for h=1: x=305 ⇒time 1h5m5s for h=2: x=610 ⇒time 2h10m10s for h=3: x=976 ⇒time 3h16m16s for h=4: x=1281 ⇒time 4h21m21s for h=5: x=1647 ⇒time 5h27m27s for h=6: x=1952 ⇒time 6h32m32s for h=7: x=2318 ⇒time 7h38m38s for h=8: x=2623 ⇒time 8h43m43s for h=9: x=2989 ⇒time 9h49m49s for h=10: x=3294 ⇒time 10h54m54s for h=11: x=3599 ⇒time 11h59m59s that means in a day there are 24 times when the three hands of a clock are at the same angular position. the picture above shows e.g. the moment 4h21m21s (am or pm) when the hands are at the same position.
$${this}\:{picture}\:{shows}\:{an}\:{analog}\:{clock}. \\ $$$${its}\:{hands}\:{don}'{t}\:{move}\:{continuously}, \\ $$$${but}\:{can}\:{only}\:{occupy}\:\mathrm{60}\:{possible} \\ $$$${angular}\:{positions}: \\ $$$$\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{58},\mathrm{59} \\ $$$$ \\ $$$${the}\:{hands}\:{move}\:{in}\:{following}\:{way}: \\ $$$${the}\:{second}'{s}\:{hand}\:{moves}\:{a}\:{step} \\ $$$${every}\:{second}.\:\:{the}\:{minute}'{s}\:{hand} \\ $$$${doesn}'{t}\:{move}\:{with}\:{each}\:{move}\:{of}\: \\ $$$${the}\:{second}'{s}\:{hand}.\:{only}\:{after}\:\mathrm{60} \\ $$$${steps}\:{of}\:{the}\:{second}'{s}\:{hand}\:\left({i}.{e}.\right. \\ $$$$\left.{after}\:\mathrm{60}\:{seconds}\right)\:{the} \\ $$$${minute}'{s}\:{hand}\:{moves}\:{a}\:{step},\:{and} \\ $$$${so}\:{on}.\:{similarly}\:{the}\:{hour}'{s}\:{hand} \\ $$$${doesn}'{t}\:{move}\:{with}\:{each}\:{move}\:{of} \\ $$$${the}\:{minute}'{s}\:{hand}.\:\:{only}\:{after} \\ $$$$\mathrm{12}\:{steps}\:{of}\:{the}\:{minute}'{s}\:{hand}\:\left({i}.{e}.\right. \\ $$$$\left.{after}\:\mathrm{12}\:{minutes}\:{or}\:\mathrm{720}\:{seconds}\right) \\ $$$${the}\:{hour}'{s}\:{hand}\:{moves}\:{a}\:{step},\:{and} \\ $$$${so}\:{on}. \\ $$$$ \\ $$$${with}\:{this}\:{knowledge}\:{about}\:{how} \\ $$$${the}\:{hands}\:{of}\:{a}\:{clock}\:{work},\:{we} \\ $$$${can}\:{determine}\:{the}\:{moments}\:{when} \\ $$$${the}\:{three}\:{hands}\:{of}\:{a}\:{clock}\:{are}\:{at} \\ $$$${the}\:{same}\:{angular}\:{position}. \\ $$$${let}'{s}\:{say}\:{the}\:{time}\:{is}\:{h}\:{o}'{clock}\:{exactly}. \\ $$$$\left(\mathrm{0}\leqslant{h}\leqslant\mathrm{11}\right).\:{at}\:{this}\:{moment}\:{the} \\ $$$${hour}'{s}\:{hand}\:{is}\:{at}\:{the}\:{position}\:\mathrm{5}{h}, \\ $$$${and}\:{the}\:{minute}'{s}\:{and}\:{second}'{s} \\ $$$${hands}\:{are}\:{at}\:{position}\:\mathrm{0}.\:{after}\:{x} \\ $$$${seconds},\:{with}\:\mathrm{0}<{x}<\mathrm{3600}, \\ $$$${the}\:{position}\:{of}\:{the} \\ $$$${second}'{s}\:{hand}\:{is}\:{mod}\left({x},\mathrm{60}\right).\:{the} \\ $$$${position}\:{of}\:{the}\:{minute}'{s}\:{hand}\:{is} \\ $$$$\lfloor\frac{{x}}{\mathrm{60}}\rfloor,\:{the}\:{position}\:{of}\:{the}\:{hour}'{s} \\ $$$${is}\:\mathrm{5}{h}+\lfloor\frac{{x}}{\mathrm{720}}\rfloor.\:{such}\:{that}\:{the}\:{three} \\ $$$${hands}\:{are}\:{at}\:{the}\:{same}\:{position}: \\ $$$$\mathrm{5}{h}+\lfloor\frac{{x}}{\mathrm{720}}\rfloor=\lfloor\frac{{x}}{\mathrm{60}}\rfloor={mod}\left({x},\mathrm{60}\right) \\ $$$$ \\ $$$${we}\:{get}\:{following}\:{results}: \\ $$$${for}\:{h}=\mathrm{0}:\:{x}=\mathrm{0}\:\Rightarrow{time}\:\mathrm{0}{h}\mathrm{0}{m}\mathrm{0}{s} \\ $$$${for}\:{h}=\mathrm{1}:\:{x}=\mathrm{305}\:\Rightarrow{time}\:\mathrm{1}{h}\mathrm{5}{m}\mathrm{5}{s} \\ $$$${for}\:{h}=\mathrm{2}:\:{x}=\mathrm{610}\:\Rightarrow{time}\:\mathrm{2}{h}\mathrm{10}{m}\mathrm{10}{s} \\ $$$${for}\:{h}=\mathrm{3}:\:{x}=\mathrm{976}\:\Rightarrow{time}\:\mathrm{3}{h}\mathrm{16}{m}\mathrm{16}{s} \\ $$$${for}\:{h}=\mathrm{4}:\:{x}=\mathrm{1281}\:\Rightarrow{time}\:\mathrm{4}{h}\mathrm{21}{m}\mathrm{21}{s} \\ $$$${for}\:{h}=\mathrm{5}:\:{x}=\mathrm{1647}\:\Rightarrow{time}\:\mathrm{5}{h}\mathrm{27}{m}\mathrm{27}{s} \\ $$$${for}\:{h}=\mathrm{6}:\:{x}=\mathrm{1952}\:\Rightarrow{time}\:\mathrm{6}{h}\mathrm{32}{m}\mathrm{32}{s} \\ $$$${for}\:{h}=\mathrm{7}:\:{x}=\mathrm{2318}\:\Rightarrow{time}\:\mathrm{7}{h}\mathrm{38}{m}\mathrm{38}{s} \\ $$$${for}\:{h}=\mathrm{8}:\:{x}=\mathrm{2623}\:\Rightarrow{time}\:\mathrm{8}{h}\mathrm{43}{m}\mathrm{43}{s} \\ $$$${for}\:{h}=\mathrm{9}:\:{x}=\mathrm{2989}\:\Rightarrow{time}\:\mathrm{9}{h}\mathrm{49}{m}\mathrm{49}{s} \\ $$$${for}\:{h}=\mathrm{10}:\:{x}=\mathrm{3294}\:\Rightarrow{time}\:\mathrm{10}{h}\mathrm{54}{m}\mathrm{54}{s} \\ $$$${for}\:{h}=\mathrm{11}:\:{x}=\mathrm{3599}\:\Rightarrow{time}\:\mathrm{11}{h}\mathrm{59}{m}\mathrm{59}{s} \\ $$$${that}\:{means}\:{in}\:{a}\:{day}\:{there}\:{are}\:\mathrm{24} \\ $$$${times}\:{when}\:{the}\:{three}\:{hands}\:{of} \\ $$$${a}\:{clock}\:{are}\:{at}\:{the}\:{same}\:{angular} \\ $$$${position}. \\ $$$${the}\:{picture}\:{above}\:{shows}\:{e}.{g}.\:{the} \\ $$$${moment}\:\mathrm{4}{h}\mathrm{21}{m}\mathrm{21}{s}\:\left({am}\:{or}\:{pm}\right) \\ $$$${when}\:{the}\:{hands}\:{are}\:{at}\:{the}\:{same} \\ $$$${position}. \\ $$
Commented by JDamian last updated on 25/Aug/19
But many other analog clocks are not so discrete − second′s hand moves quickly than one-second step (fractions of one second)
$$ \\ $$$${But}\:{many}\:{other}\:{analog}\:{clocks}\:{are}\:{not}\:{so} \\ $$$${discrete}\:−\:{second}'{s}\:{hand}\:{moves}\:{quickly}\:{than} \\ $$$${one}-{second}\:{step}\:\left({fractions}\:{of}\:{one}\:{second}\right) \\ $$
Commented by mr W last updated on 25/Aug/19
the solution depents very much on how the hands move. if it is assumed that the hands move continuously, then there is only one moment when the three hands are at the same position, i.e. at 12:00:00.
$${the}\:{solution}\:{depents}\:{very}\:{much}\:{on} \\ $$$${how}\:{the}\:{hands}\:{move}. \\ $$$${if}\:{it}\:{is}\:{assumed}\:{that}\:{the}\:{hands} \\ $$$${move}\:{continuously},\:{then}\:{there}\:{is} \\ $$$${only}\:{one}\:{moment}\:{when}\:{the}\:{three} \\ $$$${hands}\:{are}\:{at}\:{the}\:{same}\:{position}, \\ $$$${i}.{e}.\:{at}\:\mathrm{12}:\mathrm{00}:\mathrm{00}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *