Question Number 142255 by gsk2684 last updated on 28/May/21
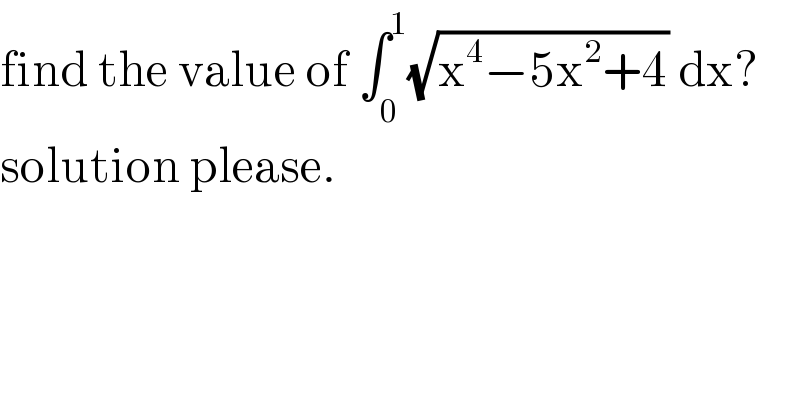
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{5x}^{\mathrm{2}} +\mathrm{4}}\:\mathrm{dx}? \\ $$$$\mathrm{solution}\:\mathrm{please}. \\ $$
Answered by mindispower last updated on 28/May/21
![by part=[x(√(x^4 −5x^2 +4))]_0 ^1 −∫_0 ^1 ((2x^4 −5x^2 )/( (√(x^4 −5x^2 +4))))dx =−2∫_0 ^1 (√(x^4 −5x^2 +4))+∫_0 ^1 ((−5x^2 +8)/( (√(x^4 −5x^2 +4))))dx ∫_0 ^1 (√(x^4 +5x^2 +4))dx=(1/3)∫_0 ^1 ((−5x^2 +8)/( (√(x^4 −5x^2 +4))))dx x^4 −5x^2 +4=(1−x^2 )(4−x^2 ) (1/3)∫_0 ^1 ((5(4−x^2 )−12)/( (√(x^2 −5x^2 +4))))dx =(5/3)∫_0 ^1 ((√(4−x^2 ))/( (√(1−x^2 ))))dx−4∫_0 ^1 (dx/( (√((1−x^2 )(4−x^2 ))))) =((10)/3)∫_0 ^1 ((√(1−(1/4)x^2 ))/( (√(1−x^2 )))) −2∫_0 ^1 (dx/( (√((1−x^2 )(1−(x^2 /4)))))) E(k^2 )=∫_0 ^1 ((√(1−k^2 x^2 ))/( (√(1−x^2 ))))dx 2nd eleptic integral K(k^2 )=∫_0 ^1 (dx/( (√(1−x^2 .(√(1−k^2 x^2 )))))) 1 st kind eleptic integral we Get∫_0 ^1 (dx/( (√(x^4 −5x^2 +4))))= ((10)/3)E((1/4))−2K((1/4))](https://www.tinkutara.com/question/Q142257.png)
$${by}\:{part}=\left[{x}\sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}}{dx} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}}{\:\sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{4}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}{dx}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}}{\:\sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}}{dx} \\ $$$${x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}=\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{4}−{x}^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{5}\left(\mathrm{4}−{x}^{\mathrm{2}} \right)−\mathrm{12}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}}{dx} \\ $$$$=\frac{\mathrm{5}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{4}−{x}^{\mathrm{2}} \right)}} \\ $$$$=\frac{\mathrm{10}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)}} \\ $$$${E}\left({k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−{k}^{\mathrm{2}} {x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:\mathrm{2}{nd}\:{eleptic}\:{integral}\: \\ $$$${K}\left({k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} .\sqrt{\mathrm{1}−{k}^{\mathrm{2}} {x}^{\mathrm{2}} }}}\:\:\mathrm{1}\:{st}\:{kind}\:{eleptic}\:{integral} \\ $$$${we}\:{Get}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}}}=\:\frac{\mathrm{10}}{\mathrm{3}}{E}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{2}{K}\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS_new last updated on 29/May/21

$$\mathrm{great}! \\ $$
Commented by mindispower last updated on 29/May/21

$${thanx}\:{sir} \\ $$
Commented by gsk2684 last updated on 31/May/21

$$\mathrm{thank}\:\mathrm{you}\: \\ $$
