Question Number 68470 by mathmax by abdo last updated on 11/Sep/19
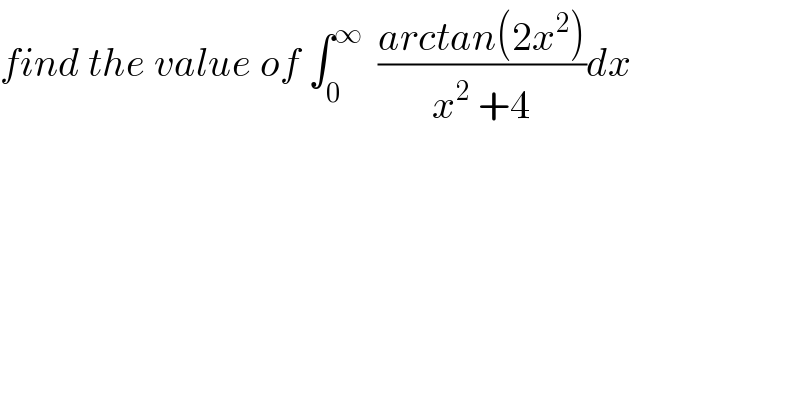
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx} \\ $$
Commented by mathmax by abdo last updated on 11/Sep/19

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\:\:{changement}\:{x}\:=\mathrm{2}{t}\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{artan}\left(\mathrm{8}{t}^{\mathrm{2}} \right)}{\mathrm{4}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\left(\mathrm{2}{dt}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{8}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left(\mathrm{8}{t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:\:{let}\:{f}\left({x}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({xt}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:{with}\:{x}\geqslant\mathrm{0} \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} \right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:\:{let}\:{W}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} {z}^{\mathrm{4}} \:+\mathrm{1}\right)} \\ $$$${W}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right){x}^{\mathrm{2}} \left({z}^{\mathrm{4}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\:=\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left({z}−{i}\right)\left({z}+{i}\right)\left({z}^{\mathrm{2}} −\frac{{i}}{{x}}\right)\left({z}^{\mathrm{2}} +\frac{{i}}{{x}}\right)} \\ $$$$=\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} \left({z}−{i}\right)\left({z}+{i}\right)\left({z}−\frac{\mathrm{1}}{\:\sqrt{{x}}\:}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${so}\:{the}\:{poles}\:{of}\:{W}\:{are}\:\overset{−} {+}{i}\:\:{and}\:\overset{−} {+}\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{and}\:\overset{−} {+}\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{{Res}\left({W},{i}\right)+{Res}\left({W},\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{Res}\left({W},−\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left({W},{i}\right)\:=\frac{−\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{2}{i}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}\:=\frac{−\mathrm{1}}{\mathrm{2}{i}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${Res}\left({W},\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{{i}}{{x}^{\mathrm{3}} \left({i}+\mathrm{1}\right)\left(\frac{\mathrm{2}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({i}+\frac{{i}}{{x}}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right){x}^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\frac{\mathrm{2}}{\:\sqrt{{x}}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$=\frac{\sqrt{{x}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}\left(\mathrm{1}+{i}\right)\left({x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \right)} \\ $$$${Res}\left({W},−\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{−{i}}{{x}^{\mathrm{3}} \left(−{i}+\mathrm{1}\right)\left(−\frac{\mathrm{2}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left(−{i}+\frac{{i}}{{x}}\right)} \\ $$$$=\frac{\sqrt{{x}}}{{x}^{\mathrm{3}} \left({i}−\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\mathrm{2}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:=\frac{\sqrt{{x}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}\left({i}−\mathrm{1}\right)\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\:−\frac{\mathrm{1}}{\mathrm{2}{i}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\sqrt{{x}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}\left(\mathrm{1}+{i}\right)\left({x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \right)}−\frac{\sqrt{{x}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}\left(\mathrm{1}−{i}\right)\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)}\right\} \\ $$$$=\mathrm{2}{i}\pi\left\{\:−\frac{\mathrm{1}}{\mathrm{2}{i}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\sqrt{{x}}\left(\mathrm{1}−{i}\right)}{\mathrm{4}\left({x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \right)}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:−\frac{\sqrt{{x}}\left(\mathrm{1}+{i}\right){e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{4}\left({x}^{\mathrm{3}} \:−{x}^{\mathrm{2}} \right)}\right\} \\ $$$$=−\frac{\pi}{{x}^{\mathrm{2}\:} +\mathrm{1}}\:+\frac{{i}\pi\left(\mathrm{1}−{i}\right)\sqrt{{x}}}{\mathrm{2}\left({x}^{\mathrm{3}} \:+{x}^{\mathrm{2}} \right)}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\:−\frac{{i}\pi\left(\mathrm{1}+{i}\right)\sqrt{{x}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} \right)} \\ $$$$….{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 11/Sep/19

$${another}\:{easy}\:{method}\:{but}\:{need}\:{a}\:{proof}\: \\ $$$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\:{let} \\ $$$$\varphi\left({z}\right)\:=\frac{{arctan}\left(\mathrm{2}{z}^{\mathrm{2}} \right)}{{z}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{arctan}\left({z}^{\mathrm{2}} \right)}{\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\mathrm{2}{i}\right)\:\:{and}\:{Res}\left(\varphi,\mathrm{2}{i}\right)\:=\frac{\mid{arctan}\left(−\mathrm{4}\right)\mid}{\mathrm{4}{i}} \\ $$$$=\frac{{arctan}\left(\mathrm{4}\right)}{\mathrm{4}{i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi×\frac{{arctan}\left(\mathrm{4}\right)}{\mathrm{4}{i}}\:=\frac{\pi}{\mathrm{2}}\:{arctan}\left(\mathrm{4}\right). \\ $$
Commented by mathmax by abdo last updated on 12/Sep/19

$$\Rightarrow{I}\:=\frac{\pi}{\mathrm{4}}{arctan}\left(\mathrm{4}\right). \\ $$
