Menu Close

find-the-value-of-0-dx-x-2-2-cos-x-1-

Tinku Tara
Pin




Question Number 65768 by mathmax by abdo last updated on 03/Aug/19
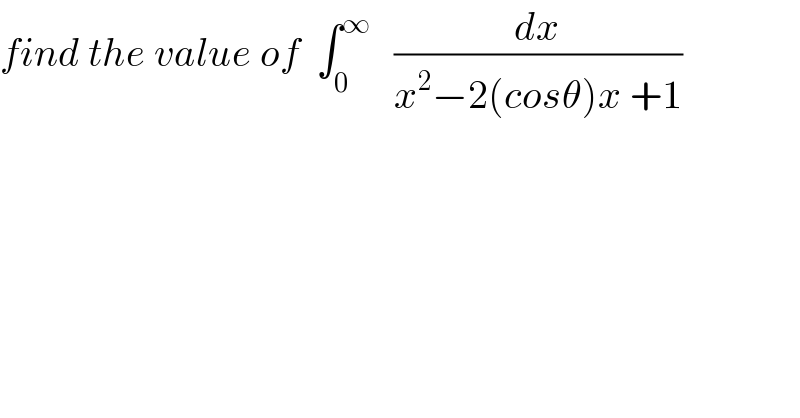
find the value of ∫_0 ^∞ (dx/(x^2 −2(cosθ)x +1))
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}\left({cos}\theta\right){x}\:+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 04/Aug/19
let I =∫_0 ^∞ (dx/(x^2 −2xcosθ +1)) ⇒I =∫_0 ^∞ (dx/(x^2 −2xcosθ +cos^2 θ +sin^2 θ)) =∫_0 ^∞ (dx/((x−cosθ)^2 +sin^2 θ)) =_(x−cosθ =∣sinθ∣u) ∫_(−((cosθ)/(∣sinθ∣))) ^(+∞) ((∣sinθ∣du)/(sin^2 θ(1+u^2 ))) =(1/(∣sinθ∣))[arctanu]_(−((cosθ)/(∣sinθ∣))) ^(+∞) =(1/(∣sinθ∣)){(π/2) +arctan(((cosθ)/(∣sinθ∣)))} case 1 sinθ>0 ⇒I =(1/(sinθ)){(π/2) +arctan((1/(tanθ)))} =(1/(sinθ)){ (π/2) +^− (π/2) −θ} case 2 sinθ<0 ⇒ I =−(1/(sinθ)){(π/2) −arctan(((cosθ)/(snθ)))} =(1/(sinθ)){−(π/2) +^− (π/2) −θ}
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta\:+\mathrm{1}}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta\:+{cos}^{\mathrm{2}} \theta\:+{sin}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({x}−{cos}\theta\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \theta}\:=_{{x}−{cos}\theta\:=\mid{sin}\theta\mid{u}} \:\:\:\:\int_{−\frac{{cos}\theta}{\mid{sin}\theta\mid}} ^{+\infty} \:\:\frac{\mid{sin}\theta\mid{du}}{{sin}^{\mathrm{2}} \theta\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mid{sin}\theta\mid}\left[{arctanu}\right]_{−\frac{{cos}\theta}{\mid{sin}\theta\mid}} ^{+\infty} \:=\frac{\mathrm{1}}{\mid{sin}\theta\mid}\left\{\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{{cos}\theta}{\mid{sin}\theta\mid}\right)\right\} \\ $$$${case}\:\mathrm{1}\:\:{sin}\theta>\mathrm{0}\:\Rightarrow{I}\:=\frac{\mathrm{1}}{{sin}\theta}\left\{\frac{\pi}{\mathrm{2}}\:+{arctan}\left(\frac{\mathrm{1}}{{tan}\theta}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{sin}\theta}\left\{\:\frac{\pi}{\mathrm{2}}\:\overset{−} {+}\frac{\pi}{\mathrm{2}}\:−\theta\right\} \\ $$$${case}\:\mathrm{2}\:\:{sin}\theta<\mathrm{0}\:\Rightarrow\:{I}\:=−\frac{\mathrm{1}}{{sin}\theta}\left\{\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{{cos}\theta}{{sn}\theta}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{{sin}\theta}\left\{−\frac{\pi}{\mathrm{2}}\:\overset{−} {+}\frac{\pi}{\mathrm{2}}\:−\theta\right\} \\ $$

Pin