Question Number 66786 by mathmax by abdo last updated on 19/Aug/19
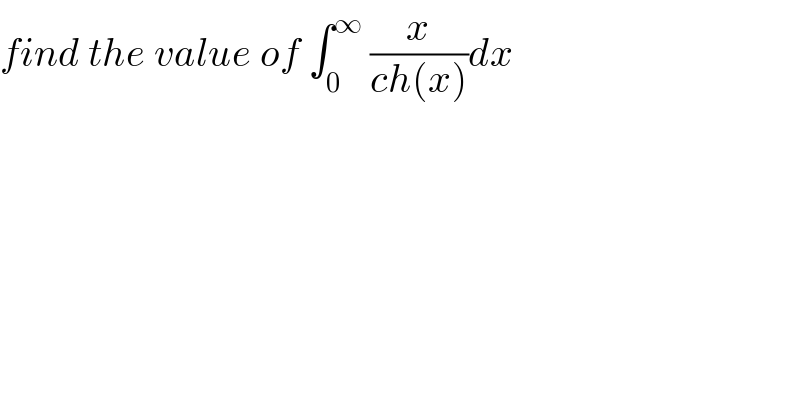
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{x}}{{ch}\left({x}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
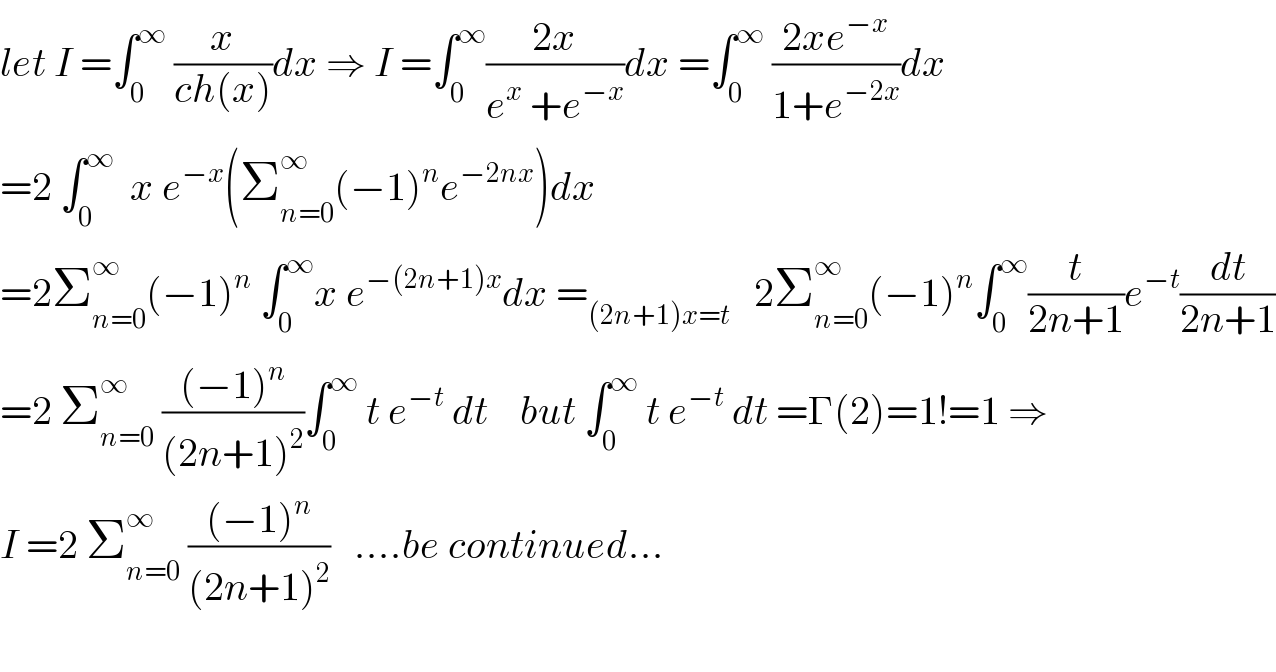
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}}{{ch}\left({x}\right)}{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}}{{e}^{{x}} \:+{e}^{−{x}} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}{xe}^{−{x}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:{x}\:{e}^{−{x}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {e}^{−\mathrm{2}{nx}} \right){dx} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} {x}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {dx}\:=_{\left(\mathrm{2}{n}+\mathrm{1}\right){x}={t}} \:\:\:\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\infty} \frac{{t}}{\mathrm{2}{n}+\mathrm{1}}{e}^{−{t}} \frac{{dt}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} \:{dt}\:\:\:\:{but}\:\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{−{t}} \:{dt}\:=\Gamma\left(\mathrm{2}\right)=\mathrm{1}!=\mathrm{1}\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:….{be}\:{continued}… \\ $$$$ \\ $$
