Menu Close

Find-the-value-of-a-2-b-2-for-a-b-real-number-such-that-a-b-1-a-1-b-1-a-and-b-a-1-b-1-a-1-b-

Tinku Tara 0 Comments
Pin




Question Number 136039 by liberty last updated on 18/Mar/21
Find the value of a^2 +b^2 for a,b real number such that a = b+(1/(a+(1/(b+(1/(a+...)))))) and b = a−(1/(b+(1/(a−(1/(b+...))))))
$${Find}\:{the}\:{value}\:{of}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \: \\ $$$${for}\:{a},{b}\:{real}\:{number}\:{such}\:{that} \\ $$$$\:{a}\:=\:{b}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{a}+…}}} \\ $$$${and}\:{b}\:=\:{a}−\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{a}−\frac{\mathrm{1}}{{b}+…}}} \\ $$
Commented by MJS_new last updated on 18/Mar/21
a^2 +b^2 =(√5)
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\sqrt{\mathrm{5}} \\ $$
Commented by liberty last updated on 18/Mar/21
how sir?
$${how}\:{sir}? \\ $$
Answered by EDWIN88 last updated on 18/Mar/21
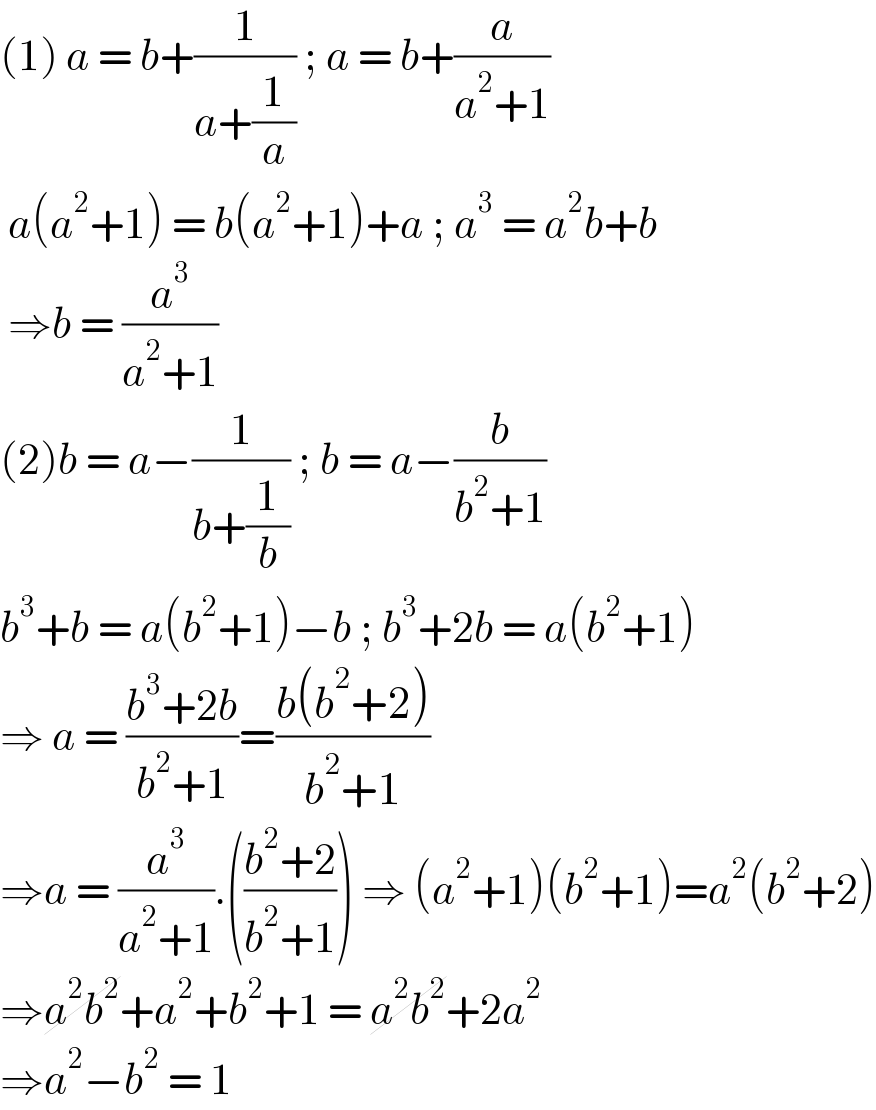
(1) a = b+(1/(a+(1/a))) ; a = b+(a/(a^2 +1)) a(a^2 +1) = b(a^2 +1)+a ; a^3 = a^2 b+b ⇒b = (a^3 /(a^2 +1)) (2)b = a−(1/(b+(1/b))) ; b = a−(b/(b^2 +1)) b^3 +b = a(b^2 +1)−b ; b^3 +2b = a(b^2 +1) ⇒ a = ((b^3 +2b)/(b^2 +1))=((b(b^2 +2))/(b^2 +1)) ⇒a = (a^3 /(a^2 +1)).(((b^2 +2)/(b^2 +1))) ⇒ (a^2 +1)(b^2 +1)=a^2 (b^2 +2) ⇒a^2 b^2 +a^2 +b^2 +1 = a^2 b^2 +2a^2 ⇒a^2 −b^2 = 1
$$\left(\mathrm{1}\right)\:{a}\:=\:{b}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}}}\:;\:{a}\:=\:{b}+\frac{{a}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:{a}\left({a}^{\mathrm{2}} +\mathrm{1}\right)\:=\:{b}\left({a}^{\mathrm{2}} +\mathrm{1}\right)+{a}\:;\:{a}^{\mathrm{3}} \:=\:{a}^{\mathrm{2}} {b}+{b} \\ $$$$\:\Rightarrow{b}\:=\:\frac{{a}^{\mathrm{3}} }{{a}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\left(\mathrm{2}\right){b}\:=\:{a}−\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{b}}}\:;\:{b}\:=\:{a}−\frac{{b}}{{b}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$${b}^{\mathrm{3}} +{b}\:=\:{a}\left({b}^{\mathrm{2}} +\mathrm{1}\right)−{b}\:;\:{b}^{\mathrm{3}} +\mathrm{2}{b}\:=\:{a}\left({b}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:{a}\:=\:\frac{{b}^{\mathrm{3}} +\mathrm{2}{b}}{{b}^{\mathrm{2}} +\mathrm{1}}=\frac{{b}\left({b}^{\mathrm{2}} +\mathrm{2}\right)}{{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{a}\:=\:\frac{{a}^{\mathrm{3}} }{{a}^{\mathrm{2}} +\mathrm{1}}.\left(\frac{{b}^{\mathrm{2}} +\mathrm{2}}{{b}^{\mathrm{2}} +\mathrm{1}}\right)\:\Rightarrow\:\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right)={a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$$\Rightarrow\cancel{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{1}\:=\:\cancel{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\mathrm{2}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:=\:\mathrm{1}\: \\ $$
Answered by MJS_new last updated on 18/Mar/21
(1) a=b+(1/(a+(1/a))) ⇔ b=(a^3 /(a^2 +1)) (2) b=a−(1/(b+(1/b))) ⇔ a(b^2 +1)−b(b^2 +2)=0 insert (1) into (2) −((a(a^4 −a^2 −1))/((a^2 +1)^3 ))=0 a=0 [rejected] a^4 −a^2 −1=0 (a^2 )^2 −(a^2 )−1=0 a^2 =((1−(√5))/2) [rejected because a∈R] ∨ a^2 =((1+(√5))/2) b^2 =(a^6 /((a^2 +1)^2 ))=−((1−(√5))/2) a^2 +b^2 =(√5)
$$\left(\mathrm{1}\right)\:{a}={b}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}}}\:\Leftrightarrow\:{b}=\frac{{a}^{\mathrm{3}} }{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\left(\mathrm{2}\right)\:{b}={a}−\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{b}}}\:\Leftrightarrow\:{a}\left({b}^{\mathrm{2}} +\mathrm{1}\right)−{b}\left({b}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{insert}\:\left(\mathrm{1}\right)\:\mathrm{into}\:\left(\mathrm{2}\right) \\ $$$$−\frac{{a}\left({a}^{\mathrm{4}} −{a}^{\mathrm{2}} −\mathrm{1}\right)}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$${a}=\mathrm{0}\:\left[\mathrm{rejected}\right] \\ $$$${a}^{\mathrm{4}} −{a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({a}^{\mathrm{2}} \right)−\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\left[\mathrm{rejected}\:\mathrm{because}\:{a}\in\mathbb{R}\right]\:\vee\:{a}^{\mathrm{2}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} =\frac{{a}^{\mathrm{6}} }{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\sqrt{\mathrm{5}} \\ $$
Answered by mr W last updated on 18/Mar/21
from (1): a=b+(1/(a+(1/a)))=b+(a/(a^2 +1)) a−b=(a/(a^2 +1))=k say ka^2 −a+k=0 a^2 =(a/(a−b))−1 from (2): b=a−(1/(b+(1/b)))=a−(b/(b^2 +1)) a−b=(b/(b^2 +1))=k kb^2 −b+k=0 b^2 =(b/(a−b))−1 a, b are roots of kx^2 −x+k=0 a+b=(1/k) ab=1 since a−b=k (a+b)^2 −4ab=k^2 (1/k^2 )−4=k^2 k^4 +4k^2 −1=0 k^2 =−2+(√5) >0 (−2−(√5) <0 rejected) k^2 +2=(√5) a^2 +b^2 =((a+b)/(a−b))−2=(1/k^2 )−2=k^2 +2=(√5) ✓ a^2 −b^2 =(a+b)(a−b)=(1/k)×k=1 ✓
$${from}\:\left(\mathrm{1}\right):\:{a}={b}+\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}}}={b}+\frac{{a}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$${a}−{b}=\frac{{a}}{{a}^{\mathrm{2}} +\mathrm{1}}={k}\:{say} \\ $$$${ka}^{\mathrm{2}} −{a}+{k}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\frac{{a}}{{a}−{b}}−\mathrm{1} \\ $$$$ \\ $$$${from}\:\left(\mathrm{2}\right):\:{b}={a}−\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{b}}}={a}−\frac{{b}}{{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$${a}−{b}=\frac{{b}}{{b}^{\mathrm{2}} +\mathrm{1}}={k} \\ $$$${kb}^{\mathrm{2}} −{b}+{k}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} =\frac{{b}}{{a}−{b}}−\mathrm{1} \\ $$$$ \\ $$$${a},\:{b}\:{are}\:{roots}\:{of}\:{kx}^{\mathrm{2}} −{x}+{k}=\mathrm{0} \\ $$$${a}+{b}=\frac{\mathrm{1}}{{k}} \\ $$$${ab}=\mathrm{1} \\ $$$${since}\:{a}−{b}={k} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{ab}={k}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{4}={k}^{\mathrm{2}} \\ $$$${k}^{\mathrm{4}} +\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${k}^{\mathrm{2}} =−\mathrm{2}+\sqrt{\mathrm{5}}\:>\mathrm{0}\:\:\:\left(−\mathrm{2}−\sqrt{\mathrm{5}}\:<\mathrm{0}\:\:{rejected}\right) \\ $$$${k}^{\mathrm{2}} +\mathrm{2}=\sqrt{\mathrm{5}} \\ $$$$ \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{{a}+{b}}{{a}−{b}}−\mathrm{2}=\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{2}={k}^{\mathrm{2}} +\mathrm{2}=\sqrt{\mathrm{5}}\:\checkmark \\ $$$$ \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left({a}+{b}\right)\left({a}−{b}\right)=\frac{\mathrm{1}}{{k}}×{k}=\mathrm{1}\:\checkmark \\ $$
Answered by ajfour last updated on 19/Mar/21
a−b=(1/(a+(1/a)))=(1/(b+(1/b))) clearly a≠b but a+(1/a)=b+(1/b) ⇒ ab=1 now (a−(1/a))(a+(1/a))=1 ⇒ a^2 −(1/a^2 )=1 a^4 −a^2 −1=0 a^2 =(((√5)+1)/2) b^2 =(1/a^2 )=(2/( (√5)+1))=(((√5)−1)/2) a^2 +b^2 =(√5)
$${a}−{b}=\frac{\mathrm{1}}{{a}+\frac{\mathrm{1}}{{a}}}=\frac{\mathrm{1}}{{b}+\frac{\mathrm{1}}{{b}}} \\ $$$${clearly}\:\:{a}\neq{b} \\ $$$${but}\:\:\:{a}+\frac{\mathrm{1}}{{a}}={b}+\frac{\mathrm{1}}{{b}} \\ $$$$\Rightarrow\:\:{ab}=\mathrm{1} \\ $$$${now}\:\:\:\left({a}−\frac{\mathrm{1}}{{a}}\right)\left({a}+\frac{\mathrm{1}}{{a}}\right)=\mathrm{1} \\ $$$$\Rightarrow\:\:\:{a}^{\mathrm{2}} −\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$${a}^{\mathrm{4}} −{a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\sqrt{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *