find-the-value-of-lim-1-cosx-tan-2x-x-

Question Number 69174 by Aditya789 last updated on 21/Sep/19

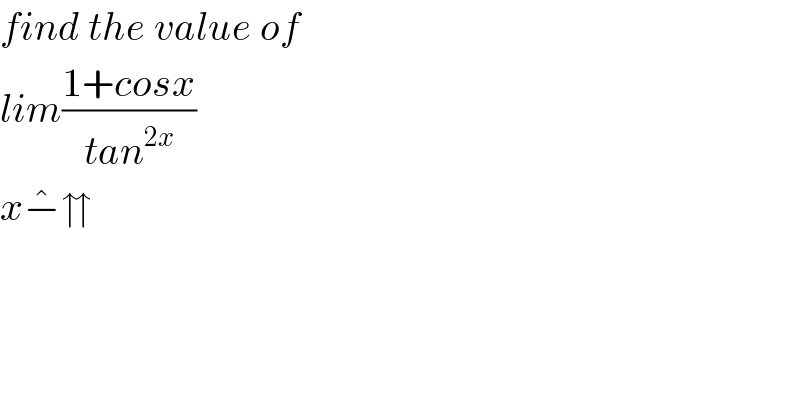
$${find}\:{the}\:{value}\:{of}\: \\ $$$${lim}\frac{\mathrm{1}+{cosx}}{{tan}^{\mathrm{2}{x}} } \\ $$$${x}\hat {−}\upuparrows \\ $$

Commented by Henri Boucatchou last updated on 21/Sep/19

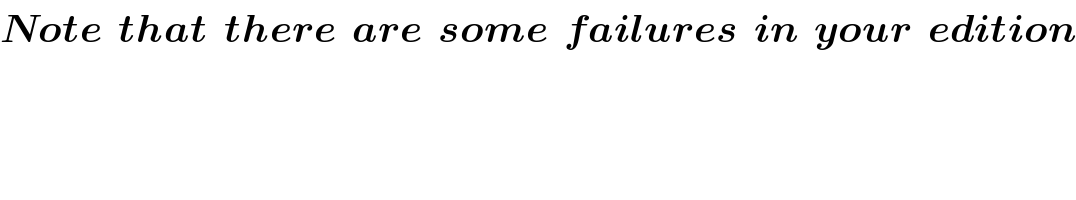
Note that there are some failures in your edition

$$\boldsymbol{{Note}}\:\:\boldsymbol{{that}}\:\:\boldsymbol{{there}}\:\:\boldsymbol{{are}}\:\:\boldsymbol{{some}}\:\:\boldsymbol{{failures}}\:\:\boldsymbol{{in}}\:\:\boldsymbol{{your}}\:\:\boldsymbol{{edition}} \\ $$

Commented by Rasheed.Sindhi last updated on 21/Sep/19

Do you mean: lim_(x→π) ((1+cosx)/( tan(2x))) Or you mean: lim_(x→π) ((1+cosx)/( tan^2 x)) ?

$${Do}\:{you}\:{mean}: \\ $$$$\underset{{x}\rightarrow\pi} {{lim}}\frac{\mathrm{1}+{cosx}}{\:\:{tan}\left(\mathrm{2}{x}\right)} \\ $$$${Or}\:{you}\:{mean}: \\ $$$$\underset{{x}\rightarrow\pi} {{lim}}\frac{\mathrm{1}+{cosx}}{\:\:{tan}^{\mathrm{2}} {x}}\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:? \\ $$

Commented by mathmax by abdo last updated on 21/Sep/19

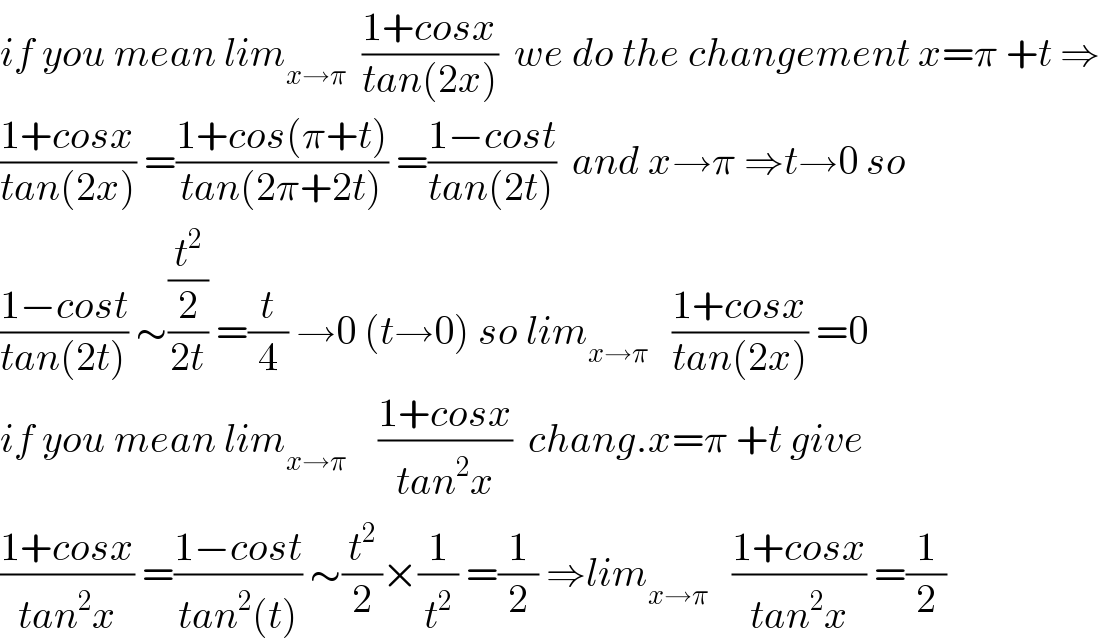
if you mean lim_(x→π) ((1+cosx)/(tan(2x))) we do the changement x=π +t ⇒ ((1+cosx)/(tan(2x))) =((1+cos(π+t))/(tan(2π+2t))) =((1−cost)/(tan(2t))) and x→π ⇒t→0 so ((1−cost)/(tan(2t))) ∼((t^2 /2)/(2t)) =(t/4) →0 (t→0) so lim_(x→π) ((1+cosx)/(tan(2x))) =0 if you mean lim_(x→π) ((1+cosx)/(tan^2 x)) chang.x=π +t give ((1+cosx)/(tan^2 x)) =((1−cost)/(tan^2 (t))) ∼(t^2 /2)×(1/t^2 ) =(1/2) ⇒lim_(x→π) ((1+cosx)/(tan^2 x)) =(1/2)

$${if}\:{you}\:{mean}\:{lim}_{{x}\rightarrow\pi} \:\:\frac{\mathrm{1}+{cosx}}{{tan}\left(\mathrm{2}{x}\right)}\:\:{we}\:{do}\:{the}\:{changement}\:{x}=\pi\:+{t}\:\Rightarrow \\ $$$$\frac{\mathrm{1}+{cosx}}{{tan}\left(\mathrm{2}{x}\right)}\:=\frac{\mathrm{1}+{cos}\left(\pi+{t}\right)}{{tan}\left(\mathrm{2}\pi+\mathrm{2}{t}\right)}\:=\frac{\mathrm{1}−{cost}}{{tan}\left(\mathrm{2}{t}\right)}\:\:{and}\:{x}\rightarrow\pi\:\Rightarrow{t}\rightarrow\mathrm{0}\:{so} \\ $$$$\frac{\mathrm{1}−{cost}}{{tan}\left(\mathrm{2}{t}\right)}\:\sim\frac{\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{\mathrm{2}{t}}\:=\frac{{t}}{\mathrm{4}}\:\rightarrow\mathrm{0}\:\left({t}\rightarrow\mathrm{0}\right)\:{so}\:{lim}_{{x}\rightarrow\pi} \:\:\:\frac{\mathrm{1}+{cosx}}{{tan}\left(\mathrm{2}{x}\right)}\:=\mathrm{0} \\ $$$${if}\:{you}\:{mean}\:{lim}_{{x}\rightarrow\pi} \:\:\:\:\frac{\mathrm{1}+{cosx}}{{tan}^{\mathrm{2}} {x}}\:\:{chang}.{x}=\pi\:+{t}\:{give} \\ $$$$\frac{\mathrm{1}+{cosx}}{{tan}^{\mathrm{2}} {x}}\:=\frac{\mathrm{1}−{cost}}{{tan}^{\mathrm{2}} \left({t}\right)}\:\sim\frac{{t}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{lim}_{{x}\rightarrow\pi} \:\:\:\frac{\mathrm{1}+{cosx}}{{tan}^{\mathrm{2}} {x}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

find-the-value-of-lim-1-cosx-tan-2x-x-

Leave a Reply Cancel reply