Menu Close

find-the-value-of-n-1-1-n-4n-2-1-2-

Tinku Tara 0 Comments
Pin




Question Number 74351 by mathmax by abdo last updated on 22/Nov/19
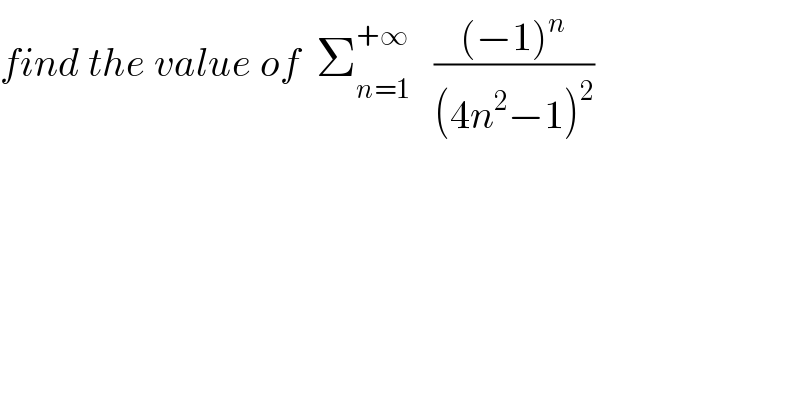
find the value of Σ_(n=1) ^(+∞) (((−1)^n )/((4n^2 −1)^2 ))
findthevalueof∑n=1+∞(−1)n(4n2−1)2
Commented by ~blr237~ last updated on 23/Nov/19
let named it S S=Σ_(n=1) ^∞ (((−1)^n )/([(2n+1)(2n−1)]^2 )) =Σ_(n=1) ^∞ (((−1)^n )/2)[(((2n+1)−(2n−1))/((2n+1)(2n−1)))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/(2n−1))−(1/(2n+1))]^2 2S=Σ_(n=1) ^∞ (−1)^n [(1/((2n−1)^2 ))−(2/((2n+1)(2n−1)))+(1/((2n+1)^2 ))] 2S=Σ_(n=1) ^∞ (((−1)^n )/((2n−1)^2 )) −Σ_(n=1) ^∞ (2/((2n+1)(2n−1)))+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) 2S=−Σ_(m=0) ^∞ (((−1)^m )/((2m+1)^2 )) −A+Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 )) with A=Σ_(n=1) ^∞ (2/((2n+1)(2n−1))) 2S=−1−A let state U_n =Σ_(k=1) ^n (2/((2k+1)(2k−1))) we have A=lim_(n→∞) U_n_ U_n =Σ_(k=1) ^n ((1/(2k−1))−(1/(2k+1)))=Σ_(k=0) ^(n−1) (1/(2k+1)) −Σ_(k=1) ^n (1/(2k+1))=1−(1/(2n+1)) So A=1 then S=−2
letnameditSS=∑∞n=1(−1)n[(2n+1)(2n−1)]2=∑∞n=1(−1)n2[(2n+1)−(2n−1)(2n+1)(2n−1)]22S=∑∞n=1(−1)n[12n−1−12n+1]22S=∑∞n=1(−1)n[1(2n−1)2−2(2n+1)(2n−1)+1(2n+1)2]2S=∑∞n=1(−1)n(2n−1)2−∑∞n=12(2n+1)(2n−1)+∑∞n=1(−1)n(2n+1)22S=−∑∞m=0(−1)m(2m+1)2−A+∑∞n=1(−1)n(2n+1)2withA=∑∞n=12(2n+1)(2n−1)2S=−1−AletstateUn=∑nk=12(2k+1)(2k−1)wehaveA=limn→∞UnUn=∑nk=1(12k−1−12k+1)=∑n−1k=012k+1−∑nk=112k+1=1−12n+1SoA=1thenS=−2

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *