Menu Close

Find-the-value-of-n-so-that-a-n-1-b-n-1-a-n-b-n-may-become-the-G-M-between-a-and-b-

Tinku Tara 0 Comments
Pin




Question Number 3465 by Rasheed Soomro last updated on 13/Dec/15
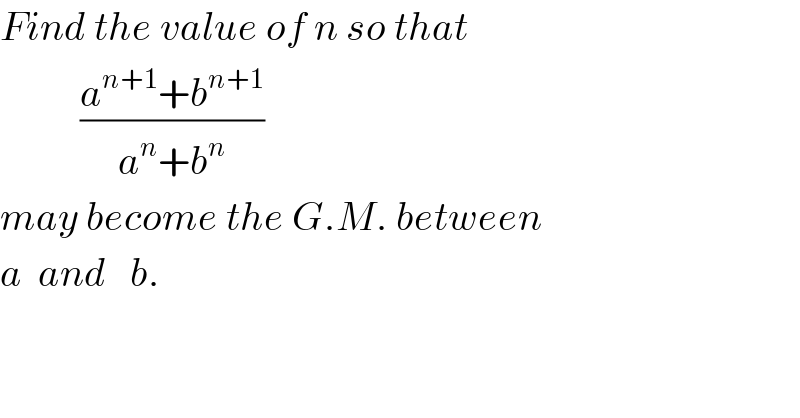
Find the value of n so that ((a^(n+1) +b^(n+1) )/(a^n +b^n )) may become the G.M. between a and b.
$${Find}\:{the}\:{value}\:{of}\:{n}\:{so}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{{a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} }{{a}^{{n}} +{b}^{{n}} } \\ $$$${may}\:{become}\:{the}\:{G}.{M}.\:{between}\: \\ $$$${a}\:\:{and}\:\:\:{b}. \\ $$
Answered by prakash jain last updated on 13/Dec/15
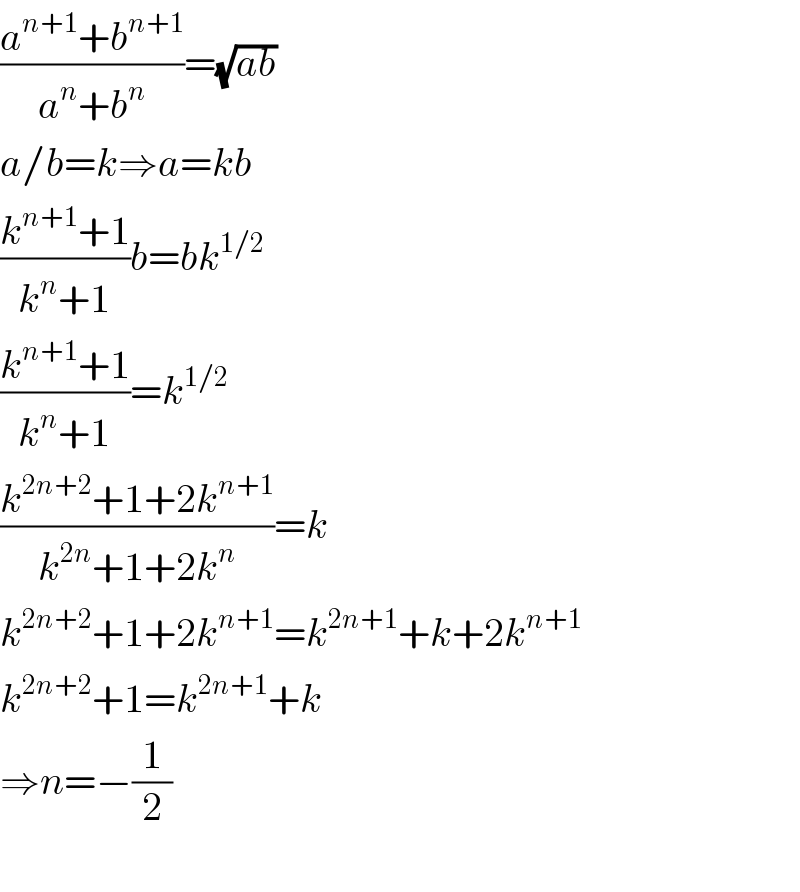
((a^(n+1) +b^(n+1) )/(a^n +b^n ))=(√(ab)) a/b=k⇒a=kb ((k^(n+1) +1)/(k^n +1))b=bk^(1/2) ((k^(n+1) +1)/(k^n +1))=k^(1/2) ((k^(2n+2) +1+2k^(n+1) )/(k^(2n) +1+2k^n ))=k k^(2n+2) +1+2k^(n+1) =k^(2n+1) +k+2k^(n+1) k^(2n+2) +1=k^(2n+1) +k ⇒n=−(1/2)
$$\frac{{a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} }{{a}^{{n}} +{b}^{{n}} }=\sqrt{{ab}} \\ $$$${a}/{b}={k}\Rightarrow{a}={kb} \\ $$$$\frac{{k}^{{n}+\mathrm{1}} +\mathrm{1}}{{k}^{{n}} +\mathrm{1}}{b}={bk}^{\mathrm{1}/\mathrm{2}} \\ $$$$\frac{{k}^{{n}+\mathrm{1}} +\mathrm{1}}{{k}^{{n}} +\mathrm{1}}={k}^{\mathrm{1}/\mathrm{2}} \\ $$$$\frac{{k}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{1}+\mathrm{2}{k}^{{n}+\mathrm{1}} }{{k}^{\mathrm{2}{n}} +\mathrm{1}+\mathrm{2}{k}^{{n}} }={k} \\ $$$${k}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{1}+\mathrm{2}{k}^{{n}+\mathrm{1}} ={k}^{\mathrm{2}{n}+\mathrm{1}} +{k}+\mathrm{2}{k}^{{n}+\mathrm{1}} \\ $$$${k}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{1}={k}^{\mathrm{2}{n}+\mathrm{1}} +{k} \\ $$$$\Rightarrow{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by prakash jain last updated on 13/Dec/15
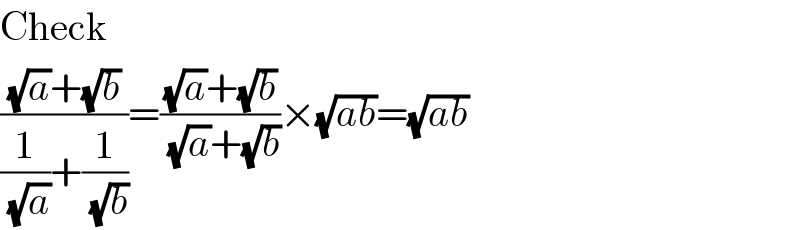
Check (((√a)+(√b))/((1/( (√a)))+(1/( (√b)))))=(((√a)+(√b))/( (√a)+(√b)))×(√(ab))=(√(ab))
$$\mathrm{Check} \\ $$$$\frac{\sqrt{{a}}+\sqrt{{b}}}{\frac{\mathrm{1}}{\:\sqrt{{a}}}+\frac{\mathrm{1}}{\:\sqrt{{b}}}}=\frac{\sqrt{{a}}+\sqrt{{b}}}{\:\sqrt{{a}}+\sqrt{{b}}}×\sqrt{{ab}}=\sqrt{{ab}} \\ $$
Answered by RasheedSindhi last updated on 14/Dec/15
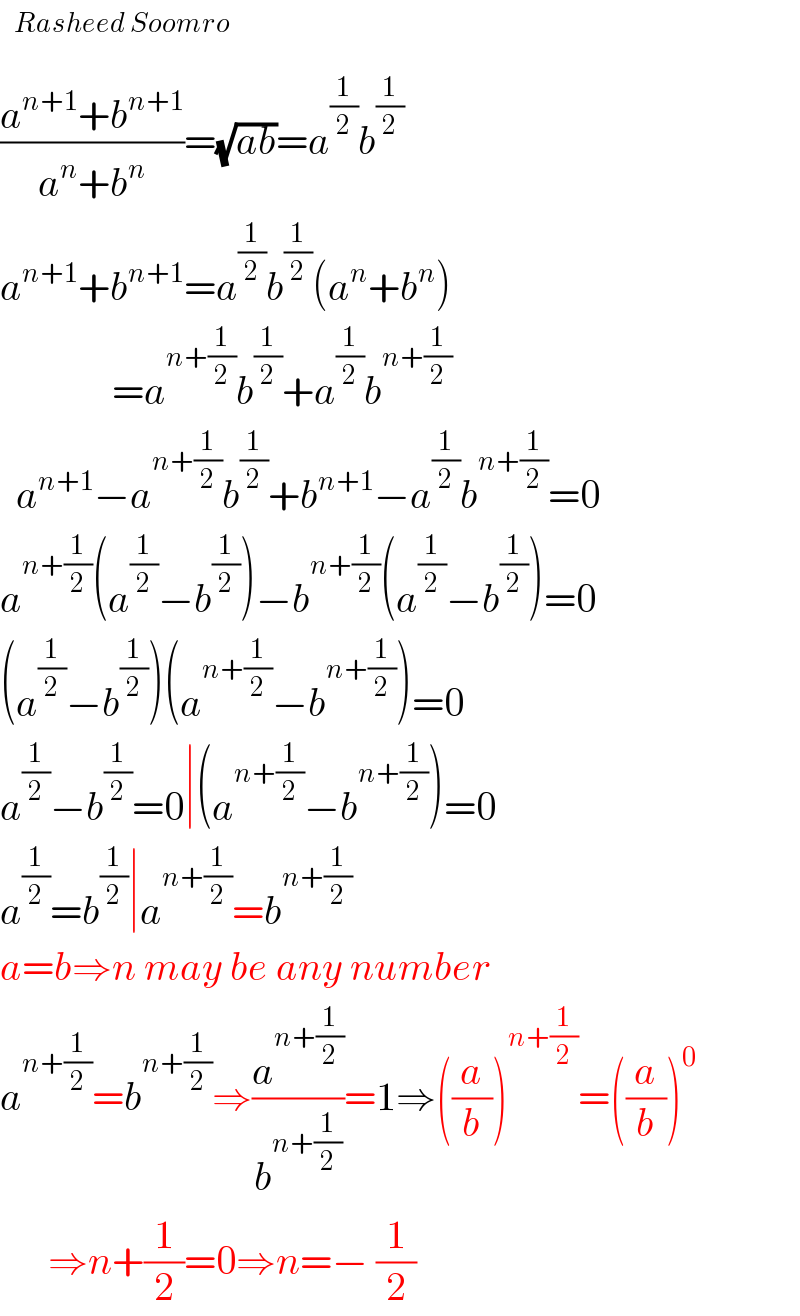
((a^(n+1) +b^(n+1) )/(a^n +b^n ))=(√(ab))=a^(1/2) b^(1/2) a^(n+1) +b^(n+1) =a^(1/2) b^(1/2) (a^n +b^n ) =a^(n+(1/2)) b^(1/2) +a^(1/2) b^(n+(1/2)) a^(n+1) −a^(n+(1/2)) b^(1/2) +b^(n+1) −a^(1/2) b^(n+(1/2)) =0 a^(n+(1/2)) (a^(1/2) −b^(1/2) )−b^(n+(1/2)) (a^(1/2) −b^(1/2) )=0 (a^(1/2) −b^(1/2) )(a^(n+(1/2)) −b^(n+(1/2)) )=0 a^(1/2) −b^(1/2) =0∣(a^(n+(1/2)) −b^(n+(1/2)) )=0 a^(1/2) =b^(1/2) ∣a^(n+(1/2)) =b^(n+(1/2)) a=b⇒n may be any number a^(n+(1/2)) =b^(n+(1/2)) ⇒(a^(n+(1/2)) /b^(n+(1/2)) )=1⇒((a/b))^(n+(1/2)) =((a/b))^0 ⇒n+(1/2)=0⇒n=− (1/2)
$$ \\ $$$$\frac{{a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} }{{a}^{{n}} +{b}^{{n}} }=\sqrt{{ab}}={a}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}^{{n}+\mathrm{1}} +{b}^{{n}+\mathrm{1}} ={a}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({a}^{{n}} +{b}^{{n}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} {b}^{\frac{\mathrm{1}}{\mathrm{2}}} +{a}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:{a}^{{n}+\mathrm{1}} −{a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} {b}^{\frac{\mathrm{1}}{\mathrm{2}}} +{b}^{{n}+\mathrm{1}} −{a}^{\frac{\mathrm{1}}{\mathrm{2}}} {b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{0} \\ $$$${a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left({a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)−{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left({a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$$\left({a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$${a}^{\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{0}\mid\left({a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} −{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \right)=\mathrm{0} \\ $$$${a}^{\frac{\mathrm{1}}{\mathrm{2}}} ={b}^{\frac{\mathrm{1}}{\mathrm{2}}} \mid{a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ={b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}={b}\Rightarrow{n}\:{may}\:{be}\:{any}\:{number} \\ $$$${a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ={b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow\frac{{a}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }{{b}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} }=\mathrm{1}\Rightarrow\left(\frac{{a}}{{b}}\right)^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} =\left(\frac{{a}}{{b}}\right)^{\mathrm{0}} \\ $$$$\:\:\:\:\:\:\Rightarrow{n}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}\Rightarrow{n}=−\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *