Question Number 68617 by Rio Michael last updated on 14/Sep/19
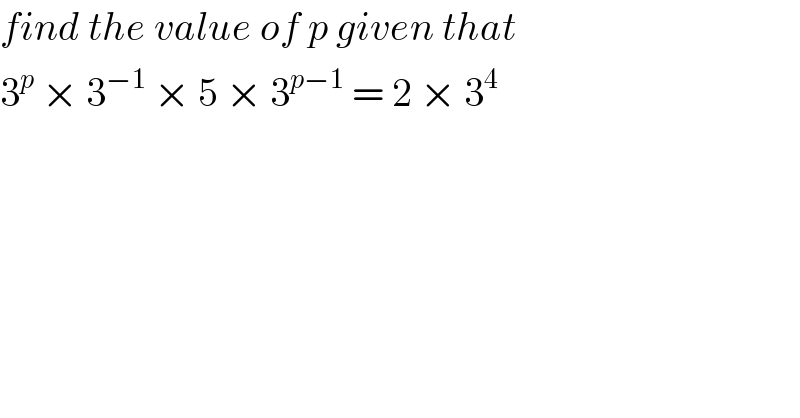
$${find}\:{the}\:{value}\:{of}\:{p}\:{given}\:{that} \\ $$$$\mathrm{3}^{{p}} \:×\:\mathrm{3}^{−\mathrm{1}} \:×\:\mathrm{5}\:×\:\mathrm{3}^{{p}−\mathrm{1}} \:=\:\mathrm{2}\:×\:\mathrm{3}^{\mathrm{4}} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Sep/19
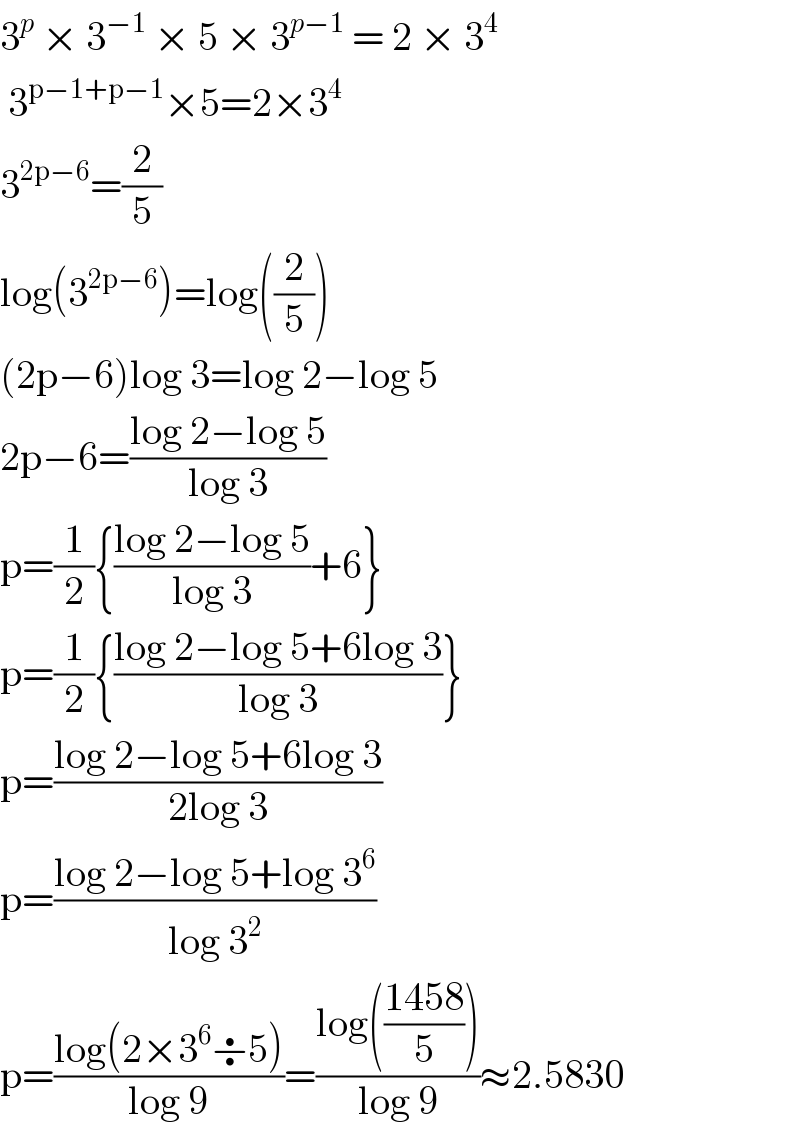
$$\mathrm{3}^{{p}} \:×\:\mathrm{3}^{−\mathrm{1}} \:×\:\mathrm{5}\:×\:\mathrm{3}^{{p}−\mathrm{1}} \:=\:\mathrm{2}\:×\:\mathrm{3}^{\mathrm{4}} \\ $$$$\:\mathrm{3}^{\mathrm{p}−\mathrm{1}+\mathrm{p}−\mathrm{1}} ×\mathrm{5}=\mathrm{2}×\mathrm{3}^{\mathrm{4}} \\ $$$$\mathrm{3}^{\mathrm{2p}−\mathrm{6}} =\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{log}\left(\mathrm{3}^{\mathrm{2p}−\mathrm{6}} \right)=\mathrm{log}\left(\frac{\mathrm{2}}{\mathrm{5}}\right) \\ $$$$\left(\mathrm{2p}−\mathrm{6}\right)\mathrm{log}\:\mathrm{3}=\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5} \\ $$$$\mathrm{2p}−\mathrm{6}=\frac{\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5}}{\mathrm{log}\:\mathrm{3}} \\ $$$$\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5}}{\mathrm{log}\:\mathrm{3}}+\mathrm{6}\right\} \\ $$$$\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5}+\mathrm{6log}\:\mathrm{3}}{\mathrm{log}\:\mathrm{3}}\right\} \\ $$$$\mathrm{p}=\frac{\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5}+\mathrm{6log}\:\mathrm{3}}{\mathrm{2log}\:\mathrm{3}} \\ $$$$\mathrm{p}=\frac{\mathrm{log}\:\mathrm{2}−\mathrm{log}\:\mathrm{5}+\mathrm{log}\:\mathrm{3}^{\mathrm{6}} }{\mathrm{log}\:\mathrm{3}^{\mathrm{2}} } \\ $$$$\mathrm{p}=\frac{\mathrm{log}\left(\mathrm{2}×\mathrm{3}^{\mathrm{6}} \boldsymbol{\div}\mathrm{5}\right)}{\mathrm{log}\:\mathrm{9}}=\frac{\mathrm{log}\left(\frac{\mathrm{1458}}{\mathrm{5}}\right)}{\mathrm{log}\:\mathrm{9}}\approx\mathrm{2}.\mathrm{5830} \\ $$
