Question Number 67342 by mathmax by abdo last updated on 26/Aug/19
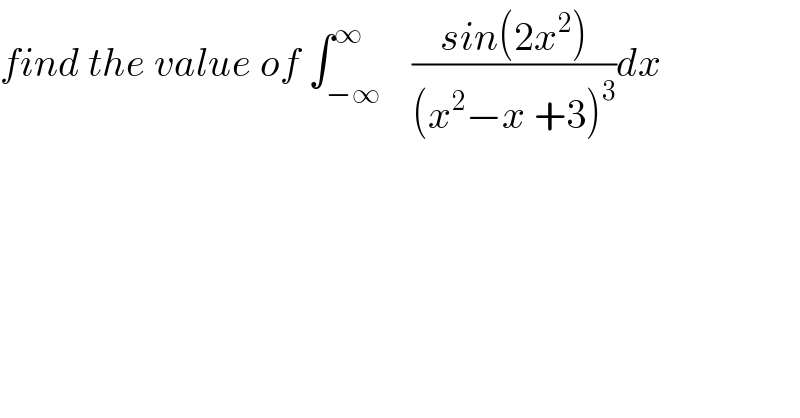
$${find}\:{the}\:{value}\:{of}\:\int_{−\infty} ^{\infty} \:\:\:\frac{{sin}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} −{x}\:+\mathrm{3}\right)^{\mathrm{3}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Aug/19

$${let}\:\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\frac{{sin}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)^{\mathrm{3}} }{dx}\:\Rightarrow\:{I}\:={Im}\:\left(\:\int_{−\infty} ^{+\infty} \:\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{z}\:+\mathrm{3}\right)^{\mathrm{3}} }{dz}\right) \\ $$$${let}\:{W}\left({z}\right)\:=\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{z}\:+\mathrm{3}\right)^{\mathrm{3}} }\:\:{poles}\:{of}\:{W}? \\ $$$${z}^{\mathrm{2}} −{z}\:+\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{1}−\mathrm{12}\:=−\mathrm{11}\:=\left({i}\sqrt{\mathrm{11}}\right)^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\Rightarrow{W}\left({z}\right)\:=\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{3}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\:\:{let}\:{apply}\:{residus}\:{theorem} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{z}_{\mathrm{1}} \right)\:\:\:\left({z}_{\mathrm{1}} {is}\:{a}\:{triple}\:{pole}\right) \\ $$$$\left.{Res}\left({W},{z}_{\mathrm{1}} \right)\:={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{3}} {W}\left({z}\right)\right\}^{\left(\mathrm{2}\right)} \right\} \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \:\:{we}\:{have} \\ $$$$\left\{\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \:=\left\{\frac{\mathrm{4}{iz}\:{e}^{\mathrm{2}{iz}^{\mathrm{2}} } \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} {e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{6}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\left\{\frac{\mathrm{4}{iz}\:{e}^{\mathrm{2}{iz}^{\mathrm{2}} } \left({z}−{z}_{\mathrm{2}} \right)−\mathrm{3}{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \:=\left\{\frac{\left(\mathrm{4}{iz}^{\mathrm{2}} −\mathrm{4}{iz}_{\mathrm{2}} {z}\right){e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\left\{\left(\mathrm{8}{iz}\:−\mathrm{4}{iz}_{\mathrm{2}} \right){e}^{\mathrm{2}{iz}^{\mathrm{2}} } \:\:\:+\mathrm{4}{iz}\:{e}^{\mathrm{2}{iz}^{\mathrm{2}} } \left(\mathrm{4}{iz}^{\mathrm{2}} −\mathrm{4}{iz}_{\mathrm{2}} {z}\right)\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} −\mathrm{4}\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} \left\{\mathrm{4}{iz}^{\mathrm{2}} −\mathrm{4}{iz}_{\mathrm{2}} {z}\right\}{e}^{\mathrm{2}{iz}^{\mathrm{2}} } \right.}{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{8}} } \\ $$$$=\frac{\left\{\left(\mathrm{8}{iz}−\mathrm{4}{iz}_{\mathrm{2}} −\mathrm{16}{z}^{\mathrm{3}} \:+\mathrm{16}{z}_{\mathrm{2}} {z}^{\mathrm{2}} \:\right)\left({z}−{z}_{\mathrm{2}} \right)−\mathrm{16}{iz}^{\mathrm{2}} \:+\mathrm{16}{iz}_{\mathrm{2}} {z}\right\}{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{5}} } \\ $$$$\mathrm{2}{Res}\left({W},{z}_{\mathrm{1}} \right)\:=\frac{\left\{\left(\mathrm{8}{iz}_{\mathrm{1}} −\mathrm{4}{iz}_{\mathrm{2}} −\mathrm{16}{z}_{\mathrm{1}} ^{\mathrm{3}} \:+\mathrm{16}{z}_{\mathrm{2}} {z}_{\mathrm{1}} ^{\mathrm{2}} \right)\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)−\mathrm{16}{iz}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{16}{iz}_{\mathrm{1}} {z}_{\mathrm{2}} \right\}{e}^{\mathrm{2}{iz}_{\mathrm{1}} ^{\mathrm{2}} } }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{5}} } \\ $$$${with}\:{z}_{\mathrm{1}} −{z}_{\mathrm{2}} ={i}\sqrt{\mathrm{11}}\:\:\:\:\:{rest}\:{to}\:{finich}\:{the}\:{calculus}… \\ $$
