Question Number 7478 by Yozzia last updated on 31/Aug/16
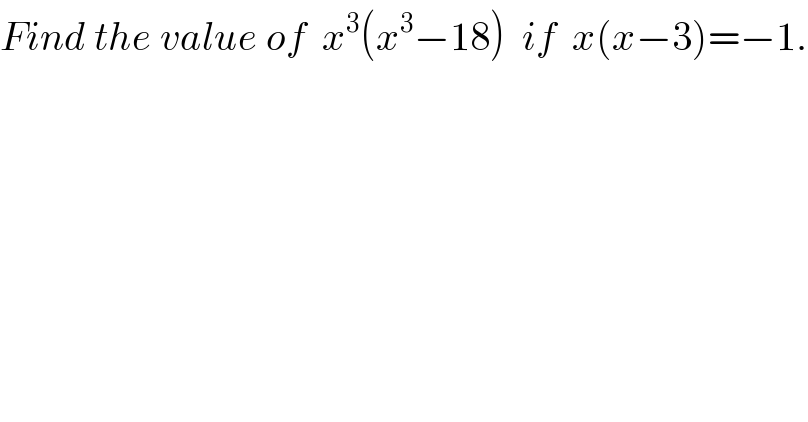
$${Find}\:{the}\:{value}\:{of}\:\:{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{18}\right)\:\:{if}\:\:{x}\left({x}−\mathrm{3}\right)=−\mathrm{1}. \\ $$
Answered by Rasheed Soomro last updated on 31/Aug/16
![x^3 (x^3 −18) if x(x−3)=−1 [x(x−3)]^3 =(−1)^3 (a−b)^3 =a^3 −b^3 −3ab(a−b) x^3 (x^3 −27−9x(x−3))=−1 x^3 (x^3 −27−9(−1)=−1 x^3 (x^3 −27+9)=−1 x^3 (x^3 −18)=−1](https://www.tinkutara.com/question/Q7481.png)
$$\:\:\:{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{18}\right)\:\:{if}\:\:{x}\left({x}−\mathrm{3}\right)=−\mathrm{1} \\ $$$$\left[{x}\left({x}−\mathrm{3}\right)\right]^{\mathrm{3}} =\left(−\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} −{b}^{\mathrm{3}} −\mathrm{3}{ab}\left({a}−{b}\right) \\ $$$${x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{27}−\mathrm{9}{x}\left({x}−\mathrm{3}\right)\right)=−\mathrm{1} \\ $$$${x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{27}−\mathrm{9}\left(−\mathrm{1}\right)=−\mathrm{1}\right. \\ $$$${x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{27}+\mathrm{9}\right)=−\mathrm{1} \\ $$$$\:{x}^{\mathrm{3}} \left({x}^{\mathrm{3}} −\mathrm{18}\right)=−\mathrm{1} \\ $$
