Question Number 9753 by j.masanja06@gmail.com last updated on 31/Dec/16
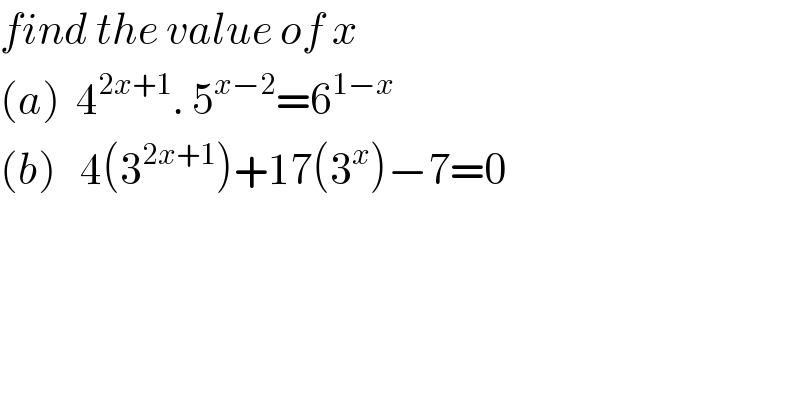
$${find}\:{the}\:{value}\:{of}\:{x} \\ $$$$\left({a}\right)\:\:\mathrm{4}^{\mathrm{2}{x}+\mathrm{1}} .\:\mathrm{5}^{{x}−\mathrm{2}} =\mathrm{6}^{\mathrm{1}−{x}} \\ $$$$\left({b}\right)\:\:\:\mathrm{4}\left(\mathrm{3}^{\mathrm{2}{x}+\mathrm{1}} \right)+\mathrm{17}\left(\mathrm{3}^{{x}} \right)−\mathrm{7}=\mathrm{0} \\ $$
Commented by ridwan balatif last updated on 31/Dec/16
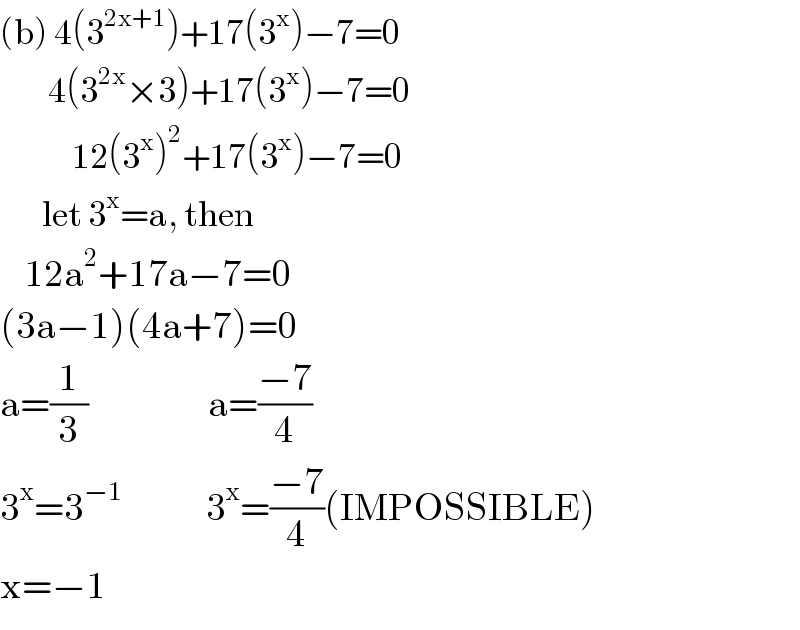
$$\left(\mathrm{b}\right)\:\mathrm{4}\left(\mathrm{3}^{\mathrm{2x}+\mathrm{1}} \right)+\mathrm{17}\left(\mathrm{3}^{\mathrm{x}} \right)−\mathrm{7}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}\left(\mathrm{3}^{\mathrm{2x}} ×\mathrm{3}\right)+\mathrm{17}\left(\mathrm{3}^{\mathrm{x}} \right)−\mathrm{7}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}\left(\mathrm{3}^{\mathrm{x}} \right)^{\mathrm{2}} +\mathrm{17}\left(\mathrm{3}^{\mathrm{x}} \right)−\mathrm{7}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{let}\:\mathrm{3}^{\mathrm{x}} =\mathrm{a},\:\mathrm{then} \\ $$$$\:\:\:\:\mathrm{12a}^{\mathrm{2}} +\mathrm{17a}−\mathrm{7}=\mathrm{0} \\ $$$$\left(\mathrm{3a}−\mathrm{1}\right)\left(\mathrm{4a}+\mathrm{7}\right)=\mathrm{0} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}=\frac{−\mathrm{7}}{\mathrm{4}} \\ $$$$\mathrm{3}^{\mathrm{x}} =\mathrm{3}^{−\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{x}} =\frac{−\mathrm{7}}{\mathrm{4}}\left(\mathrm{IMPOSSIBLE}\right) \\ $$$$\mathrm{x}=−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by ridwan balatif last updated on 31/Dec/16
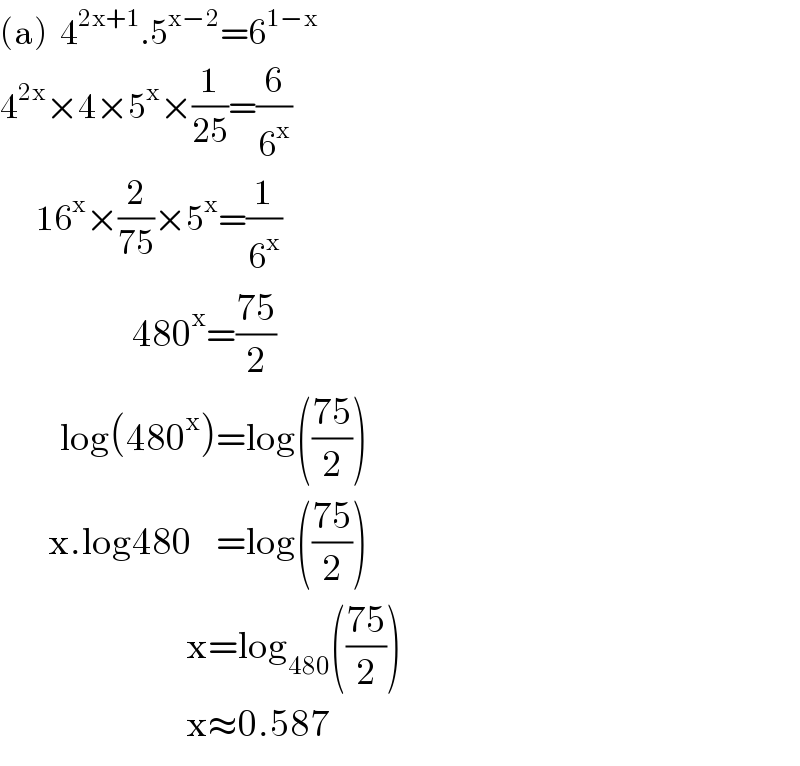
$$\left(\mathrm{a}\right)\:\:\mathrm{4}^{\mathrm{2x}+\mathrm{1}} .\mathrm{5}^{\mathrm{x}−\mathrm{2}} =\mathrm{6}^{\mathrm{1}−\mathrm{x}} \\ $$$$\mathrm{4}^{\mathrm{2x}} ×\mathrm{4}×\mathrm{5}^{\mathrm{x}} ×\frac{\mathrm{1}}{\mathrm{25}}=\frac{\mathrm{6}}{\mathrm{6}^{\mathrm{x}} } \\ $$$$\:\:\:\:\:\:\mathrm{16}^{\mathrm{x}} ×\frac{\mathrm{2}}{\mathrm{75}}×\mathrm{5}^{\mathrm{x}} =\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{x}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{480}^{\mathrm{x}} =\frac{\mathrm{75}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{log}\left(\mathrm{480}^{\mathrm{x}} \right)=\mathrm{log}\left(\frac{\mathrm{75}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}.\mathrm{log480}\:\:\:\:=\mathrm{log}\left(\frac{\mathrm{75}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{log}_{\mathrm{480}} \left(\frac{\mathrm{75}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\approx\mathrm{0}.\mathrm{587} \\ $$
