Question Number 9553 by tawakalitu last updated on 14/Dec/16
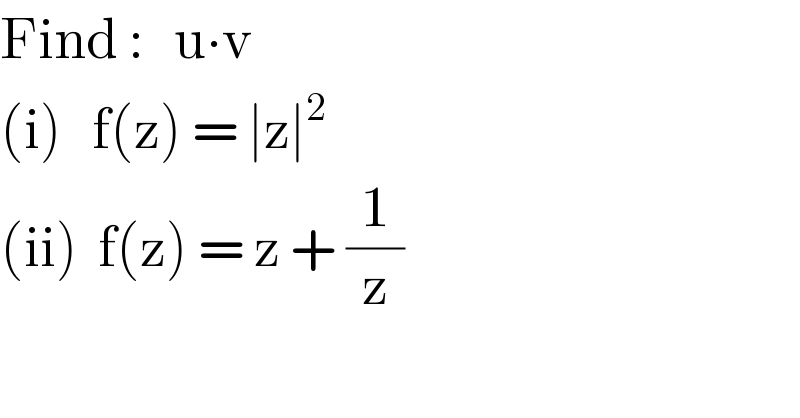
$$\mathrm{Find}\::\:\:\:\mathrm{u}\centerdot\mathrm{v} \\ $$$$\left(\mathrm{i}\right)\:\:\:\mathrm{f}\left(\mathrm{z}\right)\:=\:\mid\mathrm{z}\mid^{\mathrm{2}} \\ $$$$\left(\mathrm{ii}\right)\:\:\mathrm{f}\left(\mathrm{z}\right)\:=\:\mathrm{z}\:+\:\frac{\mathrm{1}}{\mathrm{z}} \\ $$
Commented by geovane10math last updated on 14/Dec/16

$${z}\:\mathrm{is}\:\mathrm{complex}\:? \\ $$
Commented by tawakalitu last updated on 15/Dec/16

$$\mathrm{yes}\:\mathrm{sir}. \\ $$
Commented by geovane10math last updated on 15/Dec/16
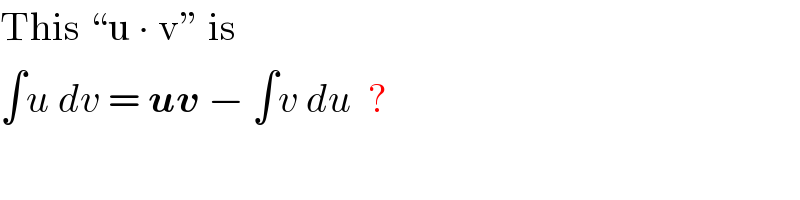
$$\mathrm{This}\:“\mathrm{u}\:\centerdot\:\mathrm{v}''\:\mathrm{is} \\ $$$$\int{u}\:{dv}\:=\:\boldsymbol{{uv}}\:−\:\int{v}\:{du}\:\:? \\ $$
