Question Number 74224 by mathmax by abdo last updated on 20/Nov/19

$${find}\:\int\:\:\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right){dx}\:\:{and} \\ $$$$\int\:\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right){dx} \\ $$
Commented by mathmax by abdo last updated on 20/Nov/19
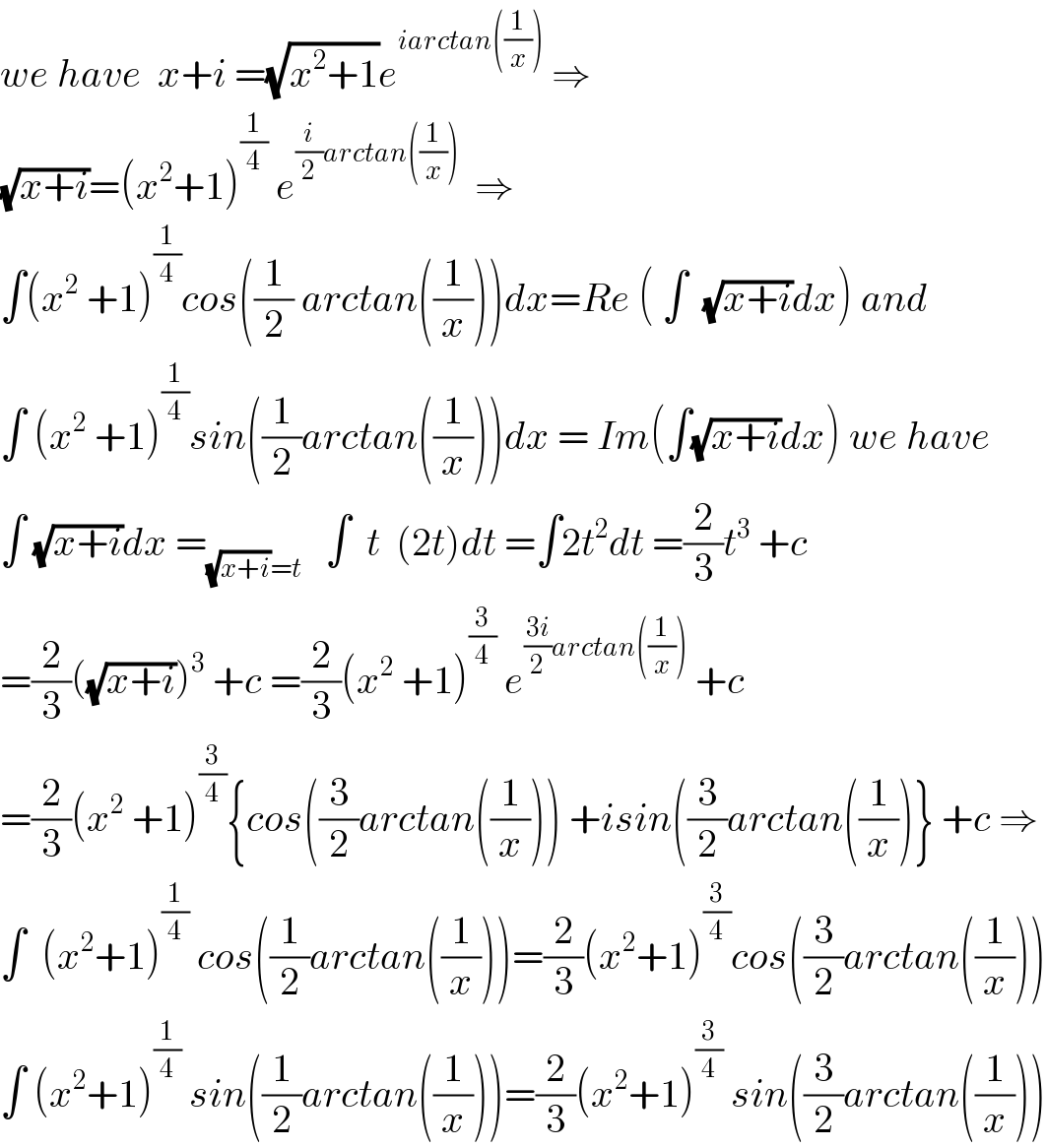
$${we}\:{have}\:\:{x}+{i}\:=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{e}^{{iarctan}\left(\frac{\mathrm{1}}{{x}}\right)} \:\Rightarrow \\ $$$$\sqrt{{x}+{i}}=\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)} \:\:\Rightarrow \\ $$$$\int\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right){dx}={Re}\:\left(\:\int\:\:\sqrt{{x}+{i}}{dx}\right)\:{and} \\ $$$$\int\:\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right){dx}\:=\:{Im}\left(\int\sqrt{{x}+{i}}{dx}\right)\:{we}\:{have} \\ $$$$\int\:\sqrt{{x}+{i}}{dx}\:=_{\sqrt{{x}+{i}}={t}} \:\:\:\int\:\:{t}\:\:\left(\mathrm{2}{t}\right){dt}\:=\int\mathrm{2}{t}^{\mathrm{2}} {dt}\:=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} \:+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{{x}+{i}}\right)^{\mathrm{3}} \:+{c}\:=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \:{e}^{\frac{\mathrm{3}{i}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)} \:+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \left\{{cos}\left(\frac{\mathrm{3}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right)\:+{isin}\left(\frac{\mathrm{3}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right\}\:+{c}\:\Rightarrow\right. \\ $$$$\int\:\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right)=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} {cos}\left(\frac{\mathrm{3}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right) \\ $$$$\int\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right)=\frac{\mathrm{2}}{\mathrm{3}}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \:{sin}\left(\frac{\mathrm{3}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right) \\ $$
Commented by mind is power last updated on 20/Nov/19

$${verry}\:{nice}\:{sir} \\ $$
Answered by mind is power last updated on 20/Nov/19
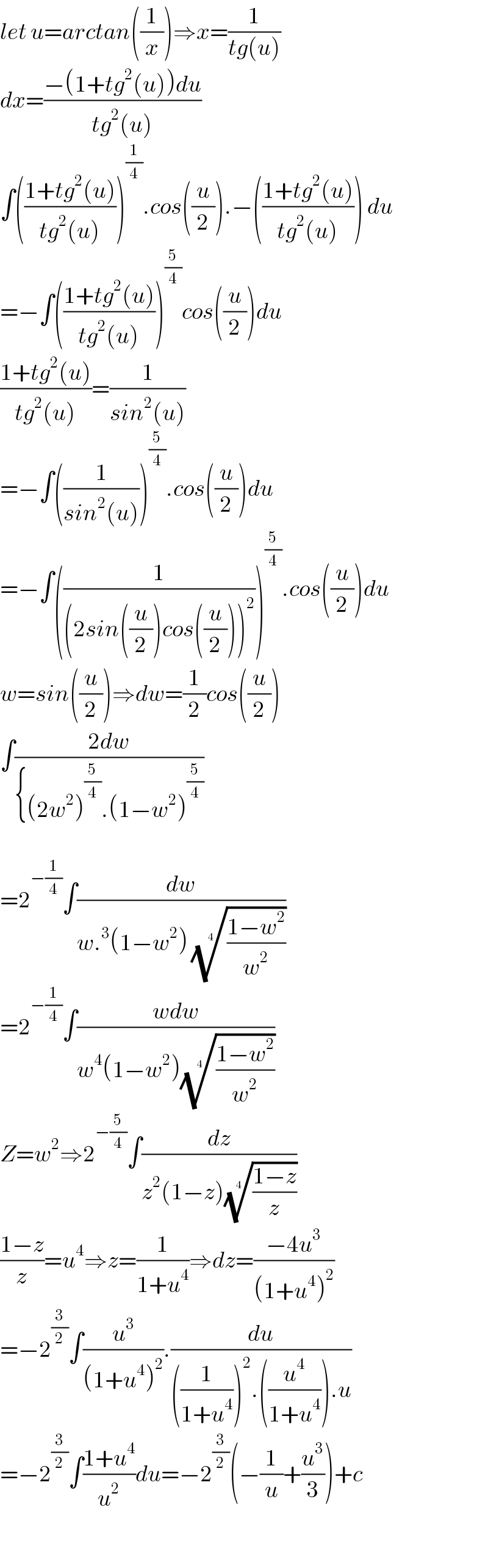
$${let}\:{u}={arctan}\left(\frac{\mathrm{1}}{{x}}\right)\Rightarrow{x}=\frac{\mathrm{1}}{{tg}\left({u}\right)} \\ $$$${dx}=\frac{−\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({u}\right)\right){du}}{{tg}^{\mathrm{2}} \left({u}\right)} \\ $$$$\int\left(\frac{\mathrm{1}+{tg}^{\mathrm{2}} \left({u}\right)}{{tg}^{\mathrm{2}} \left({u}\right)}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} .{cos}\left(\frac{{u}}{\mathrm{2}}\right).−\left(\frac{\mathrm{1}+{tg}^{\mathrm{2}} \left({u}\right)}{{tg}^{\mathrm{2}} \left({u}\right)}\right)\:{du} \\ $$$$=−\int\left(\frac{\mathrm{1}+{tg}^{\mathrm{2}} \left({u}\right)}{{tg}^{\mathrm{2}} \left({u}\right)}\right)^{\frac{\mathrm{5}}{\mathrm{4}}} {cos}\left(\frac{{u}}{\mathrm{2}}\right){du} \\ $$$$\frac{\mathrm{1}+{tg}^{\mathrm{2}} \left({u}\right)}{{tg}^{\mathrm{2}} \left({u}\right)}=\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left({u}\right)} \\ $$$$=−\int\left(\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left({u}\right)}\right)^{\frac{\mathrm{5}}{\mathrm{4}}} .{cos}\left(\frac{{u}}{\mathrm{2}}\right){du} \\ $$$$=−\int\left(\frac{\mathrm{1}}{\left(\mathrm{2}{sin}\left(\frac{{u}}{\mathrm{2}}\right){cos}\left(\frac{{u}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }\right)^{\frac{\mathrm{5}}{\mathrm{4}}} .{cos}\left(\frac{{u}}{\mathrm{2}}\right){du} \\ $$$${w}={sin}\left(\frac{{u}}{\mathrm{2}}\right)\Rightarrow{dw}=\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\frac{{u}}{\mathrm{2}}\right) \\ $$$$\int\frac{\mathrm{2}{dw}}{\left\{\left(\mathrm{2}{w}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{4}}} .\left(\mathrm{1}−{w}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{4}}} \right.} \\ $$$$ \\ $$$$=\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{4}}} \int\frac{{dw}}{{w}.^{\mathrm{3}} \left(\mathrm{1}−{w}^{\mathrm{2}} \right)\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}−{w}^{\mathrm{2}} }{{w}^{\mathrm{2}} }}} \\ $$$$=\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{4}}} \int\frac{{wdw}}{{w}^{\mathrm{4}} \left(\mathrm{1}−{w}^{\mathrm{2}} \right)\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}−{w}^{\mathrm{2}} }{{w}^{\mathrm{2}} }}} \\ $$$${Z}={w}^{\mathrm{2}} \Rightarrow\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} \int\frac{{dz}}{{z}^{\mathrm{2}} \left(\mathrm{1}−{z}\right)\sqrt[{\mathrm{4}}]{\frac{\mathrm{1}−{z}}{{z}}}} \\ $$$$\frac{\mathrm{1}−{z}}{{z}}={u}^{\mathrm{4}} \Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }\Rightarrow{dz}=\frac{−\mathrm{4}{u}^{\mathrm{3}} }{\left(\mathrm{1}+{u}^{\mathrm{4}} \right)^{\mathrm{2}} } \\ $$$$=−\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \int\frac{{u}^{\mathrm{3}} }{\left(\mathrm{1}+{u}^{\mathrm{4}} \right)^{\mathrm{2}} }.\frac{{du}}{\left(\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{4}} }\right)^{\mathrm{2}} .\left(\frac{{u}^{\mathrm{4}} }{\mathrm{1}+{u}^{\mathrm{4}} }\right).{u}} \\ $$$$=−\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \int\frac{\mathrm{1}+{u}^{\mathrm{4}} }{{u}^{\mathrm{2}} }{du}=−\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(−\frac{\mathrm{1}}{{u}}+\frac{{u}^{\mathrm{3}} }{\mathrm{3}}\right)+{c}\:\:\: \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 20/Nov/19

$${thank}\:{you}\:{sir}. \\ $$
