Menu Close

find-x-2-1-x-3-2-x-3-5x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 71802 by mathmax by abdo last updated on 20/Oct/19
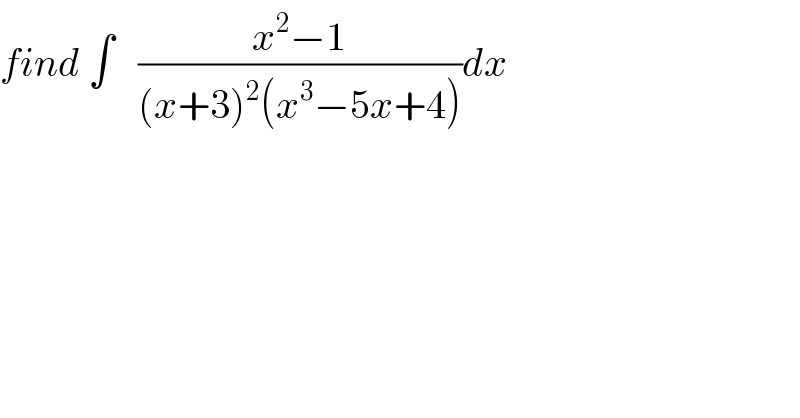
find ∫ ((x^2 −1)/((x+3)^2 (x^3 −5x+4)))dx
$${find}\:\int\:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{5}{x}+\mathrm{4}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 20/Oct/19
let I =∫((x^2 −1)/((x+3)^2 (x^3 −5x+4))) first we have x^3 −5x+4=x^3 −1−5x +5 =(x−1)(x^2 +x+1)−5(x−1) =(x−1)(x^2 +x+1−5)=(x−1)(x^2 +x−4) ⇒ I=∫ (((x−1)(x+1))/((x+3)^2 (x−1)(x^2 +x−4)))dx=∫ (dx/((x+3)^2 (x^2 +x−4))) roots of x^2 +x−4 →Δ=1−4(−4)=17 ⇒x_1 =((−1+(√(17)))/2) and x_2 =((−1−(√(17)))/2) let decompose F(x)=(1/((x+3)^2 (x^2 +x−4))) =(1/((x+3)^2 (x−x_1 )(x−x_2 ))) ⇒F(x)=(a/(x+3)) +(b/((x+3)^2 )) +(c/(x−x_1 )) +(d/(x−x_2 )) b=(1/((−3−x_1 )(−3−x_2 ))) =(1/((x_1 +3)(x_2 +3))) =(1/((((−1+(√(17)))/2)+3)(((−1−(√(17)))/2)+3))) =(4/((5+(√(17)))(5−(√(17))))) =(4/(25−17)) =(4/8) =(1/2) c=(1/((x_1 +3)^2 (x_1 −x_2 ))) =(1/((((−1+(√(17)))/2)+3)^2 ((√(17))))) =(4/( (√(17))(5+(√(17)))^2 )) d=(1/((x_2 +3)^2 (x_2 −x_1 ))) =(1/((((−1−(√(17)))/2)+3)^2 (−(√(17))))) =((−4)/( (√(17))(5−(√(17)))^2 )) F(0)=−(1/(36)) =(a/3) +(b/9)−(c/x_1 )−(d/x_2 ) ⇒−(1/(12)) =a+(b/3)−((3c)/x_1 )−((3d)/x_2 ) ⇒ a=−(1/(12))−(b/3)+((3c)/x_1 ) +((3d)/x_2 ) ⇒I=∫ F(x)dx I =aln∣x+3∣−(b/(x+3)) +cln∣x−x_1 ∣+dln∣x−x_2 ∣ +C
$${let}\:{I}\:=\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{3}} −\mathrm{5}{x}+\mathrm{4}\right)}\:{first}\:{we}\:{have} \\ $$$${x}^{\mathrm{3}} −\mathrm{5}{x}+\mathrm{4}={x}^{\mathrm{3}} −\mathrm{1}−\mathrm{5}{x}\:+\mathrm{5}\:=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\mathrm{5}\left({x}−\mathrm{1}\right) \\ $$$$=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}−\mathrm{5}\right)=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)\:\Rightarrow \\ $$$${I}=\int\:\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)}{dx}=\int\:\:\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)} \\ $$$${roots}\:{of}\:{x}^{\mathrm{2}} +{x}−\mathrm{4}\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}\left(−\mathrm{4}\right)=\mathrm{17}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$${and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}}\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)} \\ $$$$=\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{3}}\:+\frac{{b}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }\:+\frac{{c}}{{x}−{x}_{\mathrm{1}} }\:+\frac{{d}}{{x}−{x}_{\mathrm{2}} } \\ $$$${b}=\frac{\mathrm{1}}{\left(−\mathrm{3}−{x}_{\mathrm{1}} \right)\left(−\mathrm{3}−{x}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\left({x}_{\mathrm{1}} +\mathrm{3}\right)\left({x}_{\mathrm{2}} +\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}+\mathrm{3}\right)\left(\frac{−\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}}+\mathrm{3}\right)}\:=\frac{\mathrm{4}}{\left(\mathrm{5}+\sqrt{\mathrm{17}}\right)\left(\mathrm{5}−\sqrt{\mathrm{17}}\right)}\:=\frac{\mathrm{4}}{\mathrm{25}−\mathrm{17}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}=\frac{\mathrm{1}}{\left({x}_{\mathrm{1}} +\mathrm{3}\right)^{\mathrm{2}} \left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}+\mathrm{3}\right)^{\mathrm{2}} \left(\sqrt{\mathrm{17}}\right)}\:=\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}\left(\mathrm{5}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} } \\ $$$${d}=\frac{\mathrm{1}}{\left({x}_{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} \left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)}\:=\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}}+\mathrm{3}\right)^{\mathrm{2}} \left(−\sqrt{\mathrm{17}}\right)}\:=\frac{−\mathrm{4}}{\:\sqrt{\mathrm{17}}\left(\mathrm{5}−\sqrt{\mathrm{17}}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=−\frac{\mathrm{1}}{\mathrm{36}}\:=\frac{{a}}{\mathrm{3}}\:+\frac{{b}}{\mathrm{9}}−\frac{{c}}{{x}_{\mathrm{1}} }−\frac{{d}}{{x}_{\mathrm{2}} }\:\Rightarrow−\frac{\mathrm{1}}{\mathrm{12}}\:={a}+\frac{{b}}{\mathrm{3}}−\frac{\mathrm{3}{c}}{{x}_{\mathrm{1}} }−\frac{\mathrm{3}{d}}{{x}_{\mathrm{2}} }\:\Rightarrow \\ $$$${a}=−\frac{\mathrm{1}}{\mathrm{12}}−\frac{{b}}{\mathrm{3}}+\frac{\mathrm{3}{c}}{{x}_{\mathrm{1}} }\:+\frac{\mathrm{3}{d}}{{x}_{\mathrm{2}} }\:\Rightarrow{I}=\int\:{F}\left({x}\right){dx} \\ $$$${I}\:={aln}\mid{x}+\mathrm{3}\mid−\frac{{b}}{{x}+\mathrm{3}}\:+{cln}\mid{x}−{x}_{\mathrm{1}} \mid+{dln}\mid{x}−{x}_{\mathrm{2}} \mid\:+{C} \\ $$
Answered by MJS last updated on 20/Oct/19
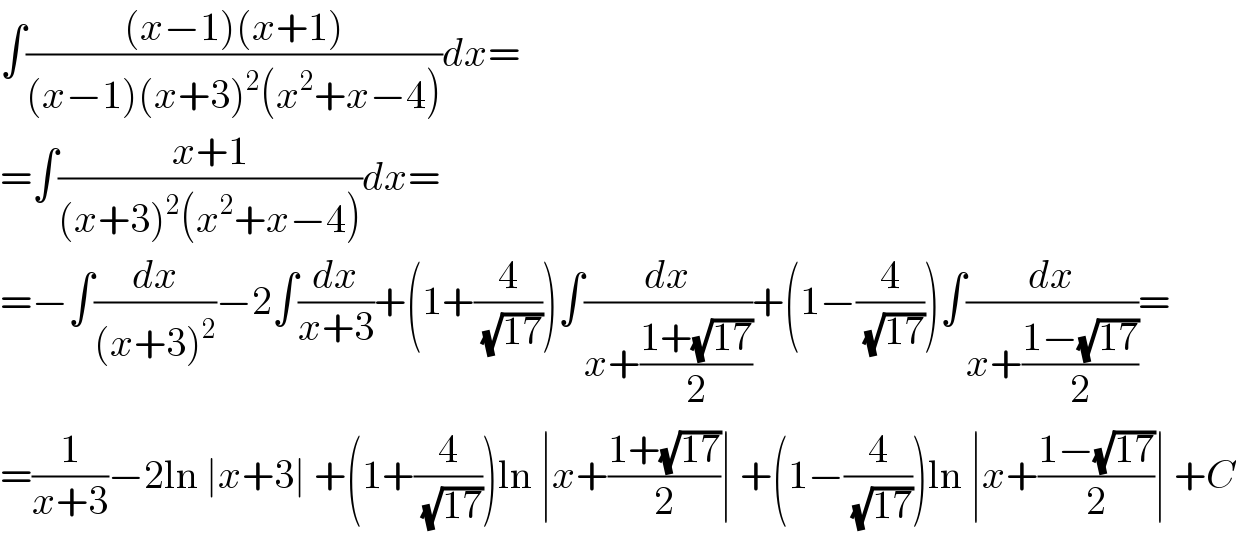
∫(((x−1)(x+1))/((x−1)(x+3)^2 (x^2 +x−4)))dx= =∫((x+1)/((x+3)^2 (x^2 +x−4)))dx= =−∫(dx/((x+3)^2 ))−2∫(dx/(x+3))+(1+(4/( (√(17)))))∫(dx/(x+((1+(√(17)))/2)))+(1−(4/( (√(17)))))∫(dx/(x+((1−(√(17)))/2)))= =(1/(x+3))−2ln ∣x+3∣ +(1+(4/( (√(17)))))ln ∣x+((1+(√(17)))/2)∣ +(1−(4/( (√(17)))))ln ∣x+((1−(√(17)))/2)∣ +C
$$\int\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)}{dx}= \\ $$$$=\int\frac{{x}+\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}−\mathrm{4}\right)}{dx}= \\ $$$$=−\int\frac{{dx}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }−\mathrm{2}\int\frac{{dx}}{{x}+\mathrm{3}}+\left(\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)\int\frac{{dx}}{{x}+\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}}+\left(\mathrm{1}−\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)\int\frac{{dx}}{{x}+\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}}}= \\ $$$$=\frac{\mathrm{1}}{{x}+\mathrm{3}}−\mathrm{2ln}\:\mid{x}+\mathrm{3}\mid\:+\left(\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)\mathrm{ln}\:\mid{x}+\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}\mid\:+\left(\mathrm{1}−\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\right)\mathrm{ln}\:\mid{x}+\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{2}}\mid\:+{C} \\ $$
Commented by mathmax by abdo last updated on 20/Oct/19
thnks sir.
$${thnks}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *