Question Number 68037 by mathmax by abdo last updated on 03/Sep/19
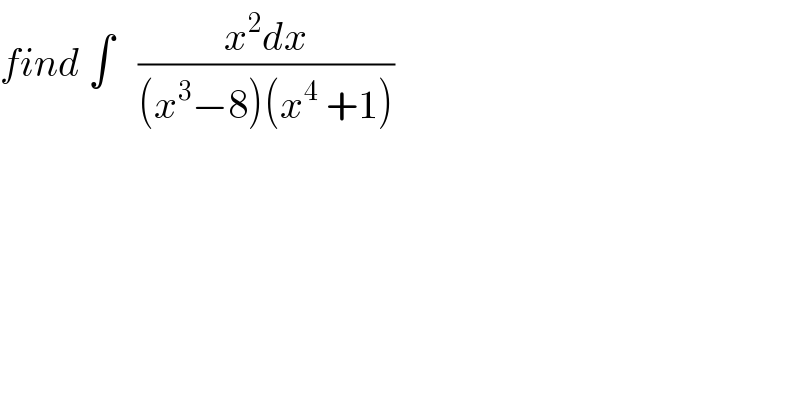
$${find}\:\int\:\:\:\frac{{x}^{\mathrm{2}} {dx}}{\left({x}^{\mathrm{3}} −\mathrm{8}\right)\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)} \\ $$
Answered by MJS last updated on 04/Sep/19
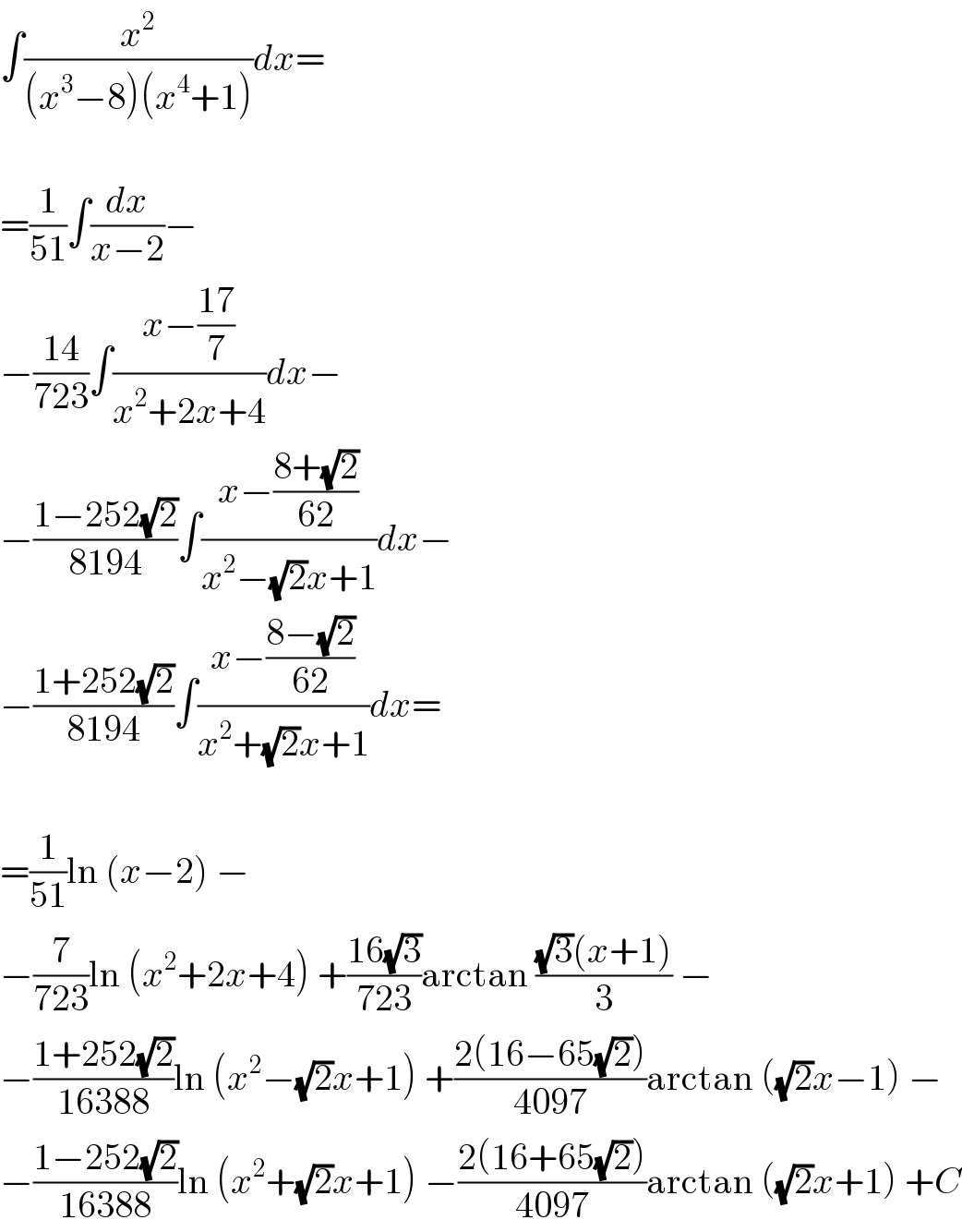
$$\int\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} −\mathrm{8}\right)\left({x}^{\mathrm{4}} +\mathrm{1}\right)}{dx}= \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{51}}\int\frac{{dx}}{{x}−\mathrm{2}}− \\ $$$$−\frac{\mathrm{14}}{\mathrm{723}}\int\frac{{x}−\frac{\mathrm{17}}{\mathrm{7}}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}{dx}− \\ $$$$−\frac{\mathrm{1}−\mathrm{252}\sqrt{\mathrm{2}}}{\mathrm{8194}}\int\frac{{x}−\frac{\mathrm{8}+\sqrt{\mathrm{2}}}{\mathrm{62}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}− \\ $$$$−\frac{\mathrm{1}+\mathrm{252}\sqrt{\mathrm{2}}}{\mathrm{8194}}\int\frac{{x}−\frac{\mathrm{8}−\sqrt{\mathrm{2}}}{\mathrm{62}}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}= \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{51}}\mathrm{ln}\:\left({x}−\mathrm{2}\right)\:− \\ $$$$−\frac{\mathrm{7}}{\mathrm{723}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)\:+\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{723}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)}{\mathrm{3}}\:− \\ $$$$−\frac{\mathrm{1}+\mathrm{252}\sqrt{\mathrm{2}}}{\mathrm{16388}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:+\frac{\mathrm{2}\left(\mathrm{16}−\mathrm{65}\sqrt{\mathrm{2}}\right)}{\mathrm{4097}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}−\mathrm{1}\right)\:− \\ $$$$−\frac{\mathrm{1}−\mathrm{252}\sqrt{\mathrm{2}}}{\mathrm{16388}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:−\frac{\mathrm{2}\left(\mathrm{16}+\mathrm{65}\sqrt{\mathrm{2}}\right)}{\mathrm{4097}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:+{C} \\ $$
Commented by turbo msup by abdo last updated on 04/Sep/19
$${thank}\:{you}\:{sir}\:{mjs} \\ $$
