Menu Close

find-x-2-x-x-4-x-2-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 78267 by msup trace by abdo last updated on 15/Jan/20
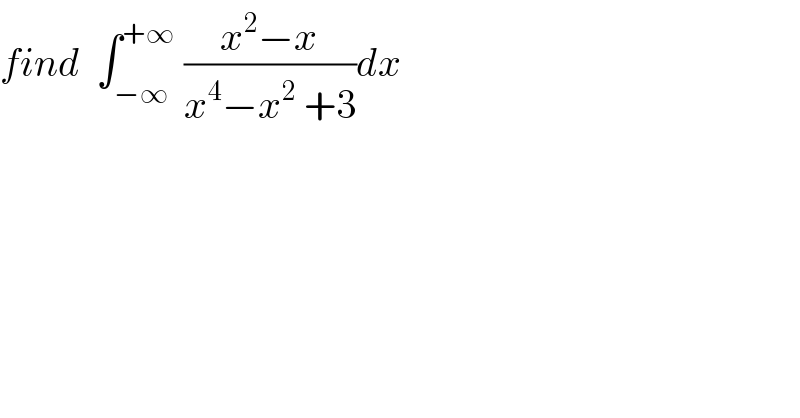
find ∫_(−∞) ^(+∞) ((x^2 −x)/(x^4 −x^2 +3))dx
$${find}\:\:\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$
Commented by mathmax by abdo last updated on 17/Jan/20
let A =∫_(−∞) ^(+∞) ((x^2 −x)/(x^4 −x^2 +3))dx ⇒ A =∫_(−∞) ^(+∞) (x^2 /(x^4 −x^2 +3))dx−∫_(−∞) ^(+∞) ((xdx)/(x^4 −x^2 +3))(→odd) =∫_(−∞) ^(+∞) (x^2 /(x^4 −x^2 +3))dx let W(z)=(z^2 /(z^4 −z^2 +3)) poles of W? z^4 −z^2 +3 =0 ⇒t^2 −t+3 =0 (t=z^2 ) Δ=1−12 =−11 ⇒t_1 =((1+i(√(11)))/2) and t_2 =((1−i(√(11)))/2) ∣t_1 ∣ =(1/2)(√(1+11))=(1/2)(2(√3)) =(√3) ⇒t_1 =(√3)e^(iarctan((√(11)))) t_2 =conj(t_1 )=(√3)e^(−iarctan((√(11)))) ⇒W(z)=(z^2 /((z^2 −(√3)e^(iarctan((√(11)))) (z^2 −(√3)e^(−iarctan((√(11)))) ))) =(z^2 /((z−α e^((i/2)arctan((√(11)))) )(z+αe^((i/2)arctan((√(11)))) )(z−αe^(−(i/2)arctan((√(11)))) )(z+αe^(−(i/2)arctan((√(11)))) ))) (with α =(√(√3))) ∫_(−∞) ^(+∞) W(z)dz =2iπ{ Res(W,αe^((i/2)arctan((√(11)))) )+Res(W,−αe^(−(i/2)arctan((√(11)))) )} Res(W,αe^((i/2)arctan((√(11)))) ) =((α^2 e^(iarctan((√(11)))) )/(2αe^((i/2)arctan((√(11)))) (α^2 e^(iarctan((√(11)))) −α^2 e^(−iarctan((√(11)))) ))) =(1/(2α))×(e^((i/2)arctan((√(11)))) /(2i sin(arctan((√(11)))))) =(1/(4iαsin(arctan((√(11)))))×e^((i/2)arctan((√(11)))) ....be continued...
$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}\:\Rightarrow\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}−\int_{−\infty} ^{+\infty} \:\frac{{xdx}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}\left(\rightarrow{odd}\right) \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx}\:\:{let}\:{W}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{3}}\:\:{poles}\:{of}\:{W}? \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{3}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} −{t}+\mathrm{3}\:=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{12}\:=−\mathrm{11}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$$\mid{t}_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{11}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\:=\sqrt{\mathrm{3}}\:\Rightarrow{t}_{\mathrm{1}} =\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \\ $$$${t}_{\mathrm{2}} ={conj}\left({t}_{\mathrm{1}} \right)=\sqrt{\mathrm{3}}{e}^{−{iarctan}\left(\sqrt{\mathrm{11}}\right)} \:\Rightarrow{W}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} −\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \left({z}^{\mathrm{2}} −\sqrt{\mathrm{3}}{e}^{−{iarctan}\left(\sqrt{\mathrm{11}}\right)} \right)\right.} \\ $$$$=\frac{{z}^{\mathrm{2}} }{\left({z}−\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\left({z}+\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\left({z}−\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\left({z}+\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)} \\ $$$$\left({with}\:\alpha\:=\sqrt{\sqrt{\mathrm{3}}}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)+{Res}\left({W},−\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\right\} \\ $$$${Res}\left({W},\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\:=\frac{\alpha^{\mathrm{2}} \:{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} }{\mathrm{2}\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \left(\alpha^{\mathrm{2}} \:{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} −\alpha^{\mathrm{2}} {e}^{−{iarctan}\left(\sqrt{\mathrm{11}}\right)} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\alpha}×\frac{{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} }{\mathrm{2}{i}\:{sin}\left({arctan}\left(\sqrt{\mathrm{11}}\right)\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}\alpha{sin}\left({arctan}\left(\sqrt{\mathrm{11}}\right)\right.}×{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \\ $$$$….{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *