Menu Close

find-x-3-x-3-3-x-2-7-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 137694 by Mathspace last updated on 05/Apr/21
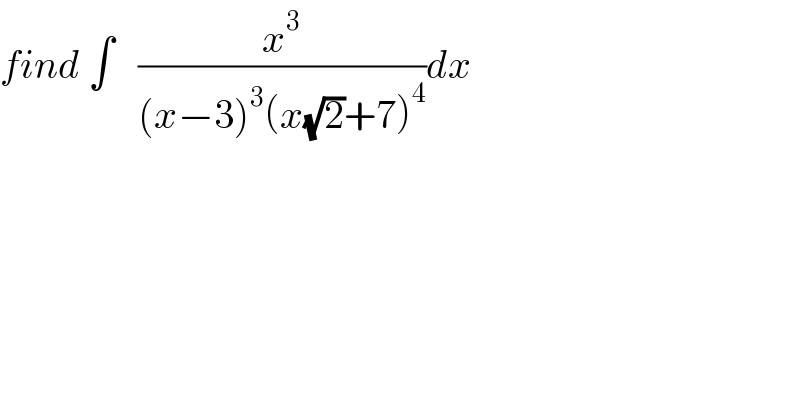
find ∫ (x^3 /((x−3)^3 (x(√2)+7)^4 ))dx
$${find}\:\int\:\:\:\frac{{x}^{\mathrm{3}} }{\left({x}−\mathrm{3}\right)^{\mathrm{3}} \left({x}\sqrt{\mathrm{2}}+\mathrm{7}\right)^{\mathrm{4}} }{dx} \\ $$
Commented by MJS_new last updated on 05/Apr/21
you can either decompose or apply Ostrogradski′s Method; it′s no fun typing with these constants...
$$\mathrm{you}\:\mathrm{can}\:\mathrm{either}\:\mathrm{decompose}\:\mathrm{or}\:\mathrm{apply}\:\mathrm{Ostrogradski}'\mathrm{s} \\ $$$$\mathrm{Method};\:\mathrm{it}'\mathrm{s}\:\mathrm{no}\:\mathrm{fun}\:\mathrm{typing}\:\mathrm{with}\:\mathrm{these}\:\mathrm{constants}… \\ $$
Commented by MJS_new last updated on 05/Apr/21
if you want to study the methods try ∫(x^3 /((x−1)^3 (x+1)^4 ))dx= =−(((x^2 +x+4)(3x^2 −1))/(48(x−1)^2 (x+1)^3 ))+(1/(32))ln ∣((x+1)/(x−1))∣ +C your example uses the same path with nasty constants ∫(x^3 /((x−3)^3 ((√2)x+7)^4 ))dx= =(((1109519964−784602612(√2))x^4 −(18723385548−13239011439(√2))x^3 +(116325008541−82282349527(√2))x^2 −(314307560196−222235080396(√2))x+311134260024−219840177123(√2))/(171774906(x−3)^2 ((√2)x+7)^3 ))+((9(115502365−81673862(√2)))/(887503681))ln ∣((x−3)/( (√2)x+7))∣ +C please check for typos if you can
$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{study}\:\mathrm{the}\:\mathrm{methods}\:\mathrm{try} \\ $$$$\int\frac{{x}^{\mathrm{3}} }{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{1}\right)^{\mathrm{4}} }{dx}= \\ $$$$=−\frac{\left({x}^{\mathrm{2}} +{x}+\mathrm{4}\right)\left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{48}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{32}}\mathrm{ln}\:\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\mid\:+{C} \\ $$$$\mathrm{your}\:\mathrm{example}\:\mathrm{uses}\:\mathrm{the}\:\mathrm{same}\:\mathrm{path}\:\mathrm{with}\:\mathrm{nasty}\:\mathrm{constants} \\ $$$$\int\frac{{x}^{\mathrm{3}} }{\left({x}−\mathrm{3}\right)^{\mathrm{3}} \left(\sqrt{\mathrm{2}}{x}+\mathrm{7}\right)^{\mathrm{4}} }{dx}= \\ $$$$=\frac{\left(\mathrm{1109519964}−\mathrm{784602612}\sqrt{\mathrm{2}}\right){x}^{\mathrm{4}} −\left(\mathrm{18723385548}−\mathrm{13239011439}\sqrt{\mathrm{2}}\right){x}^{\mathrm{3}} +\left(\mathrm{116325008541}−\mathrm{82282349527}\sqrt{\mathrm{2}}\right){x}^{\mathrm{2}} −\left(\mathrm{314307560196}−\mathrm{222235080396}\sqrt{\mathrm{2}}\right){x}+\mathrm{311134260024}−\mathrm{219840177123}\sqrt{\mathrm{2}}}{\mathrm{171774906}\left({x}−\mathrm{3}\right)^{\mathrm{2}} \left(\sqrt{\mathrm{2}}{x}+\mathrm{7}\right)^{\mathrm{3}} }+\frac{\mathrm{9}\left(\mathrm{115502365}−\mathrm{81673862}\sqrt{\mathrm{2}}\right)}{\mathrm{887503681}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{3}}{\:\sqrt{\mathrm{2}}{x}+\mathrm{7}}\mid\:+{C} \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{for}\:\mathrm{typos}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can} \\ $$
Commented by mathmax by abdo last updated on 06/Apr/21
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mathmax by abdo last updated on 06/Apr/21
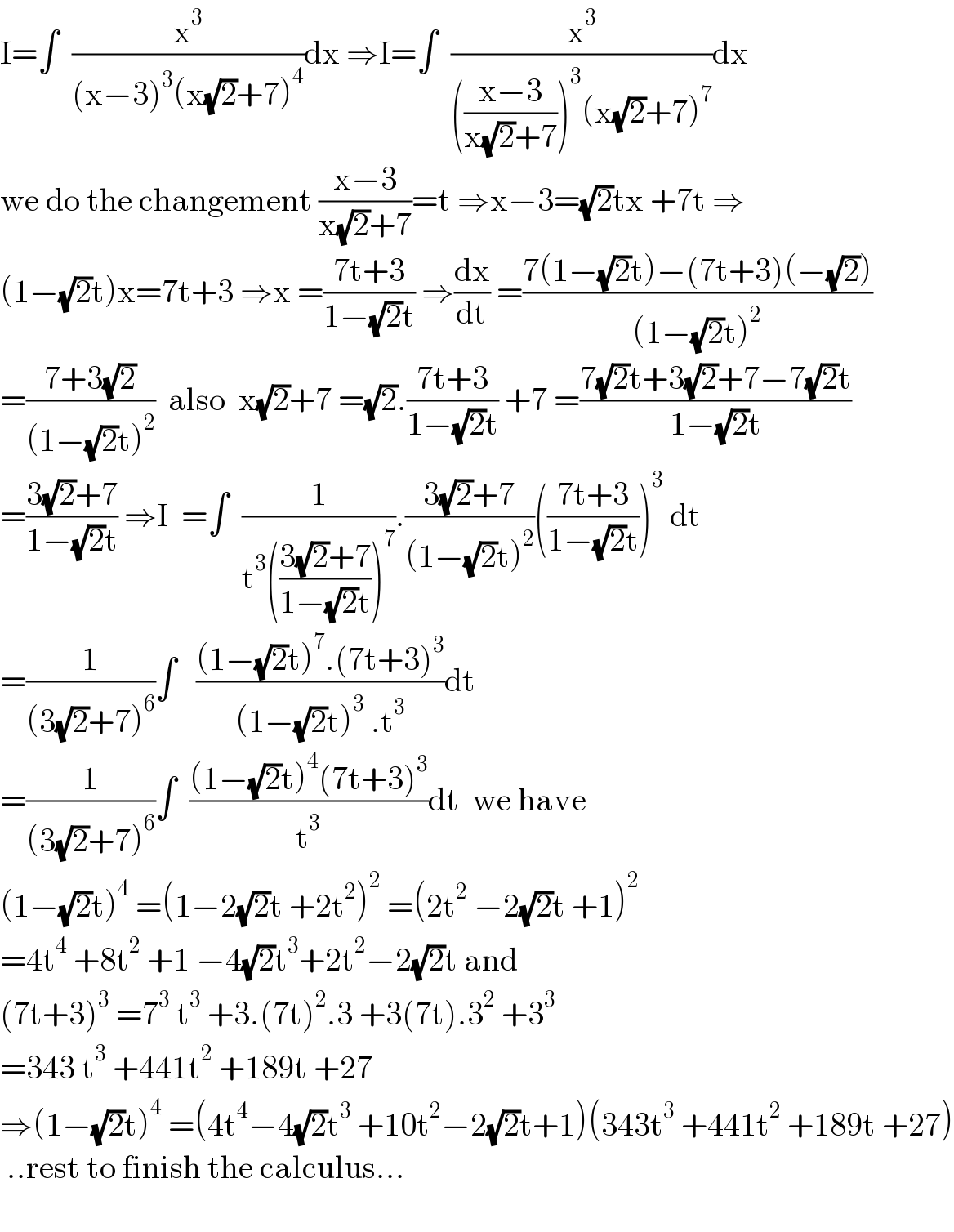
I=∫ (x^3 /((x−3)^3 (x(√2)+7)^4 ))dx ⇒I=∫ (x^3 /((((x−3)/(x(√2)+7)))^3 (x(√2)+7)^7 ))dx we do the changement ((x−3)/(x(√2)+7))=t ⇒x−3=(√2)tx +7t ⇒ (1−(√2)t)x=7t+3 ⇒x =((7t+3)/(1−(√2)t)) ⇒(dx/dt) =((7(1−(√2)t)−(7t+3)(−(√2)))/((1−(√2)t)^2 )) =((7+3(√2))/((1−(√2)t)^2 )) also x(√2)+7 =(√2).((7t+3)/(1−(√2)t)) +7 =((7(√2)t+3(√2)+7−7(√2)t)/(1−(√2)t)) =((3(√2)+7)/(1−(√2)t)) ⇒I =∫ (1/(t^3 (((3(√2)+7)/(1−(√2)t)))^7 )).((3(√2)+7)/((1−(√2)t)^2 ))(((7t+3)/(1−(√2)t)))^3 dt =(1/((3(√2)+7)^6 ))∫ (((1−(√2)t)^7 .(7t+3)^3 )/((1−(√2)t)^3 .t^3 ))dt =(1/((3(√2)+7)^6 ))∫ (((1−(√2)t)^4 (7t+3)^3 )/t^3 )dt we have (1−(√2)t)^4 =(1−2(√2)t +2t^2 )^2 =(2t^2 −2(√2)t +1)^2 =4t^4 +8t^2 +1 −4(√2)t^3 +2t^2 −2(√2)t and (7t+3)^3 =7^3 t^3 +3.(7t)^2 .3 +3(7t).3^2 +3^3 =343 t^3 +441t^2 +189t +27 ⇒(1−(√2)t)^4 =(4t^4 −4(√2)t^3 +10t^2 −2(√2)t+1)(343t^3 +441t^2 +189t +27) ..rest to finish the calculus...
$$\mathrm{I}=\int\:\:\frac{\mathrm{x}^{\mathrm{3}} }{\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{3}} \left(\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{7}\right)^{\mathrm{4}} }\mathrm{dx}\:\Rightarrow\mathrm{I}=\int\:\:\frac{\mathrm{x}^{\mathrm{3}} }{\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{7}}\right)^{\mathrm{3}} \left(\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{7}\right)^{\mathrm{7}} }\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{7}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{3}=\sqrt{\mathrm{2}}\mathrm{tx}\:+\mathrm{7t}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)\mathrm{x}=\mathrm{7t}+\mathrm{3}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{7t}+\mathrm{3}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{7}\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)−\left(\mathrm{7t}+\mathrm{3}\right)\left(−\sqrt{\mathrm{2}}\right)}{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{2}}}{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{2}} }\:\:\mathrm{also}\:\:\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{7}\:=\sqrt{\mathrm{2}}.\frac{\mathrm{7t}+\mathrm{3}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}}\:+\mathrm{7}\:=\frac{\mathrm{7}\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}−\mathrm{7}\sqrt{\mathrm{2}}\mathrm{t}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}}\:\Rightarrow\mathrm{I}\:\:=\int\:\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} \left(\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}}\right)^{\mathrm{7}} }.\frac{\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}}{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{2}} }\left(\frac{\mathrm{7t}+\mathrm{3}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}}\right)^{\mathrm{3}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}\right)^{\mathrm{6}} }\int\:\:\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{7}} .\left(\mathrm{7t}+\mathrm{3}\right)^{\mathrm{3}} }{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{3}} \:.\mathrm{t}^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{3}\sqrt{\mathrm{2}}+\mathrm{7}\right)^{\mathrm{6}} }\int\:\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{4}} \left(\mathrm{7t}+\mathrm{3}\right)^{\mathrm{3}} }{\mathrm{t}^{\mathrm{3}} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{4}} \:=\left(\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\:+\mathrm{2t}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\left(\mathrm{2t}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\:+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\mathrm{4t}^{\mathrm{4}} \:+\mathrm{8t}^{\mathrm{2}} \:+\mathrm{1}\:−\mathrm{4}\sqrt{\mathrm{2}}\mathrm{t}^{\mathrm{3}} +\mathrm{2t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}\:\mathrm{and}\: \\ $$$$\left(\mathrm{7t}+\mathrm{3}\right)^{\mathrm{3}} \:=\mathrm{7}^{\mathrm{3}} \:\mathrm{t}^{\mathrm{3}} \:+\mathrm{3}.\left(\mathrm{7t}\right)^{\mathrm{2}} .\mathrm{3}\:+\mathrm{3}\left(\mathrm{7t}\right).\mathrm{3}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{3}} \\ $$$$=\mathrm{343}\:\mathrm{t}^{\mathrm{3}} \:+\mathrm{441t}^{\mathrm{2}} \:+\mathrm{189t}\:+\mathrm{27} \\ $$$$\Rightarrow\left(\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{t}\right)^{\mathrm{4}} \:=\left(\mathrm{4t}^{\mathrm{4}} −\mathrm{4}\sqrt{\mathrm{2}}\mathrm{t}^{\mathrm{3}} \:+\mathrm{10t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{1}\right)\left(\mathrm{343t}^{\mathrm{3}} \:+\mathrm{441t}^{\mathrm{2}} \:+\mathrm{189t}\:+\mathrm{27}\right) \\ $$$$\:..\mathrm{rest}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{the}\:\mathrm{calculus}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *