find-x-and-y-2x-y-x-y-1-log-2-y-x-

Question Number 73191 by Mr. K last updated on 07/Nov/19

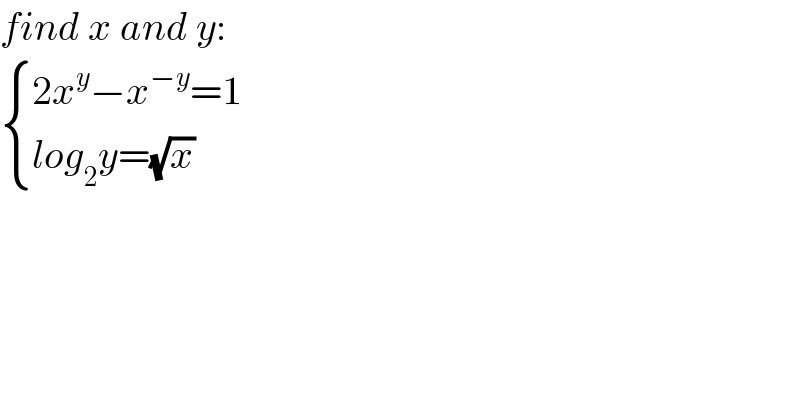
f i n d x a n d y :

{\begin{cases} 2 x^{y} - x^{- y} = 1 \\ {l o g}_{2} y = \sqrt{x} \end{cases}

Answered by mind is power last updated on 07/Nov/19

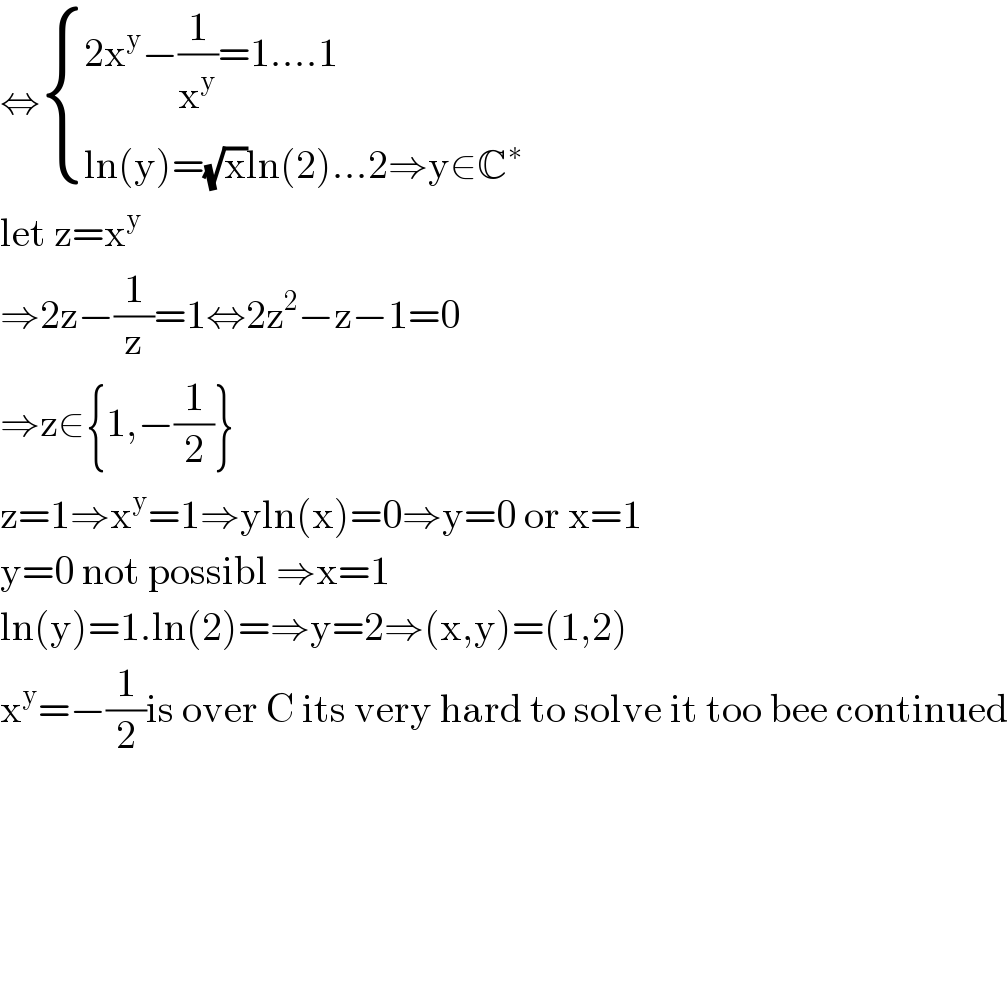
\Leftrightarrow {\begin{cases} {2 x}^{y} - \frac{1}{x^{y}} = 1 \dots . 1 \\ \ln (y) = \sqrt{x} \ln (2) \dots 2 \Rightarrow y \in C^{*} \end{cases}

let z = x^{y}

\Rightarrow 2 z - \frac{1}{z} = 1 \Leftrightarrow {2 z}^{2} - z - 1 = 0

\Rightarrow z \in {1, - \frac{1}{2}}

z = 1 \Rightarrow x^{y} = 1 \Rightarrow yln (x) = 0 \Rightarrow y = 0 or x = 1

y = 0 not possibl \Rightarrow x = 1

\ln (y) = 1 . \ln (2) =\Rightarrow y = 2 \Rightarrow (x, y) = (1, 2)

x^{y} = - \frac{1}{2} is over C its very hard to solve it too bee continued