Question Number 73032 by mathmax by abdo last updated on 05/Nov/19
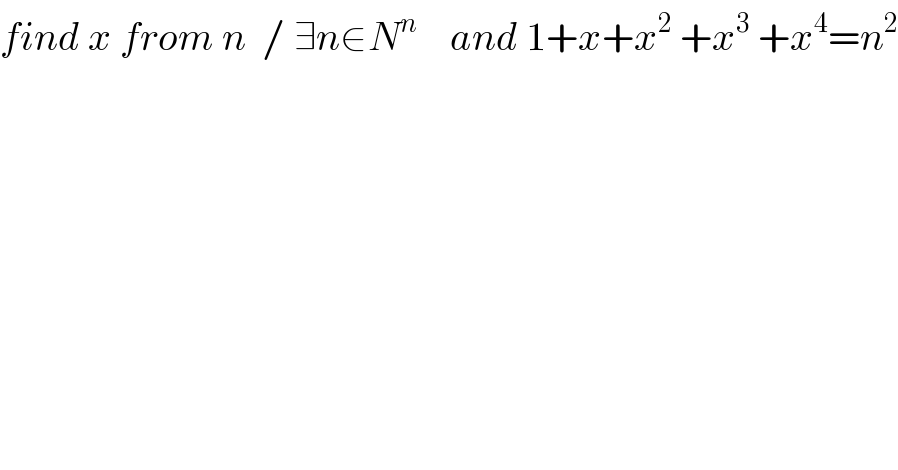
$${find}\:{x}\:{from}\:{n}\:\:/\:\exists{n}\in{N}^{{n}} \:\:\:\:{and}\:\mathrm{1}+{x}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{3}} \:+{x}^{\mathrm{4}} ={n}^{\mathrm{2}} \\ $$
Answered by mind is power last updated on 05/Nov/19

$$\Leftrightarrow\mathrm{4}+\mathrm{4x}+\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} =\left(\mathrm{2n}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4x}^{\mathrm{4}} +\mathrm{5x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{2x}+\mathrm{1}\geqslant\mathrm{4}+\mathrm{4x}+\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{3}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)\geqslant\mathrm{0}\Rightarrow\mathrm{x}\geqslant\mathrm{3} \\ $$$$\mathrm{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{solution}\: \\ $$$$\mathrm{x}=\mathrm{1}\:\mathrm{not} \\ $$$$\mathrm{x}=\mathrm{2}\:\:\mathrm{not} \\ $$$$\mathrm{lets}\:\mathrm{assum}\:\mathrm{x}\geqslant\mathrm{3} \\ $$$$\Rightarrow\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \geqslant\mathrm{4}+\mathrm{4x}+\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{4}} \\ $$$$\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} =\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} \leqslant\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}+\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{2n}\right)^{\mathrm{2}} =\left(\mathrm{2x}+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3}, \\ $$$$\mathrm{2n}=\left(\mathrm{6}+\mathrm{4}\right)\Rightarrow\mathrm{n}=\mathrm{5} \\ $$$$\left(\mathrm{x},\mathrm{n}\right)\in\left\{\left(\mathrm{0},\mathrm{1}\right),\left(\mathrm{3},\mathrm{5}\right)\right\} \\ $$$$ \\ $$$$ \\ $$
Commented by mind is power last updated on 06/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 05/Nov/19

$${thank}\:{you}\:{sir}. \\ $$
