Menu Close

Find-x-n-n-Z-satisfying-x-0-0-x-1-1-and-x-n-1-x-n-x-n-1-2-1-x-n-1-x-n-2-1-for-n-1-

Tinku Tara 0 Comments
Pin




Question Number 7532 by Yozzia last updated on 02/Sep/16
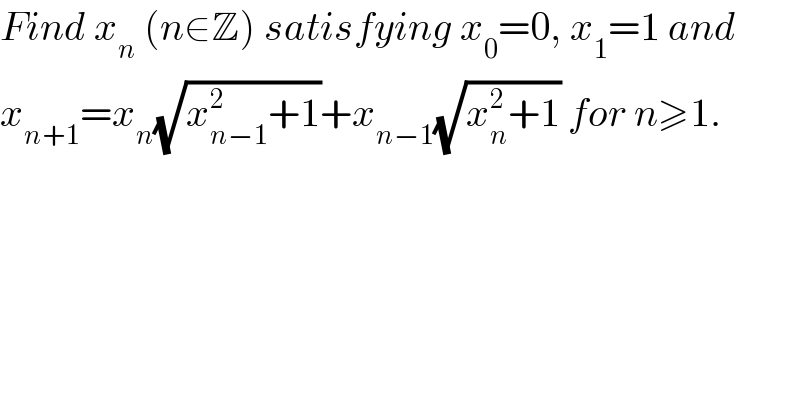
Find x_n (n∈Z) satisfying x_0 =0, x_1 =1 and x_(n+1) =x_n (√(x_(n−1) ^2 +1))+x_(n−1) (√(x_n ^2 +1)) for n≥1.
$${Find}\:{x}_{{n}} \:\left({n}\in\mathbb{Z}\right)\:{satisfying}\:{x}_{\mathrm{0}} =\mathrm{0},\:{x}_{\mathrm{1}} =\mathrm{1}\:{and} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} \sqrt{{x}_{{n}−\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}}+{x}_{{n}−\mathrm{1}} \sqrt{{x}_{{n}} ^{\mathrm{2}} +\mathrm{1}}\:{for}\:{n}\geqslant\mathrm{1}. \\ $$
Commented by sou1618 last updated on 03/Sep/16
when n=1 x_2 =1 when n=2 x_3 =2(√2) when n=3 x_4 =2(√2)(√2)+(√(8+1))=7 ... when n>2 x_n ,x_(n−1) >1 x_(n+1) =x_n (√(x_(n−1) ^2 +1))+x_(n−1) (√(x_n ^2 +1))∙∙∙(∗) x_n =(1/2)(y_n −(1/y_n ))(y_n ≥1) (1/2)(y_(n+1) −y_(n+1) ^(−1) )=(1/2)(y_n −y_n ^(−1) )(1/2)(y_(n−1) +y_(n−1) ^(−1) )+(1/2)(y_(n−1) −y_(n−1) ^(−1) )(1/2)(y_n +y_n ^(−1) ) 2(y_(n+1) −y_(n+1) ^(−1) )=(y_n −y_n ^(−1) )(y_(n−1) +y_(n−1) ^(−1) )+(y_(n−1) −y_(n−1) ^(−1) )(y_n +y_n ^(−1) ) 2(y_(n+1) −y_(n+1) ^(−1) )=2y_n y_(n−1) −2y_n ^(−1) y_n ^(−1) y_(n+1) −(1/y_(n+1) )=y_n y_(n−1) −(1/(y_n y_(n−1) )) y_(n+1) ^2 −(y_n y_(n−1) −(1/(y_n y_(n−1) )))y_(n+1) −1=0 (y_(n+1) −y_n y_(n−1) )(y_(n+1) +(1/(y_n y_(n−1) )))=0 y_(n+1) =y_n y_(n−1) (∵y_n >0) x_0 =0,y_0 ^2 −0y_0 −1=0 y_0 =1 x_1 =1,y_1 ^2 −2y_1 −1=0 y_1 =1+(√2) y_n =y_(n−1) y_(n−2) =y_(n−2) ^2 y_(n−3) =y_(n−3) ^3 y_(n−4) ^2 =y_(n−4) ^5 y_(n−5) ^3 =... y_2 =1(1+(√2)),y_3 =(1+(√2))^2 ,y_4 =(1+(√2))^3 ,y_5 =(1+(√2))^5 ... 1 1 2 3 5 8 13 21...fibonacci y_n =(1+(√2))^(f(n)) { ((f(n)=f(n−1)+f(n−2))),((f(0)=0,f(1)=1)) :} f(n)=(1/( (√5))){(((1+(√5))/2))^n −(((1−(√5))/2))^n } =((φ^n −(−φ)^(−n) )/( (√5))),(φ=((1+(√5))/2)) x_n =(1/2){(1+(√2))^(f(n)) −(1+(√2))^(−f(n)) } ++++++++++++ x_0 =(1/2){(1+(√2))^0 −(1+(√2))^0 }=0 x_1 =(1/2){1+(√2)−(1/(1+(√2)))}=(((1+(√2))^2 −1^2 )/(2(1+(√2))))=1 x_2 =x_1 =1 x_3 =(1/2){(1+(√2))^2 −(1/((1+(√2))^2 ))}=((((1+(√2))^2 )^2 −1^2 )/(2(1+(√2))^2 )) =(((3+2(√2)+1)(3+2(√2)−1))/(2(1+(√2))^2 )) =(((2(√2)(1+(√2)))(2(1+(√2))))/(2(1+(√2))^2 ))=2(√2) ...
$${when}\:{n}=\mathrm{1} \\ $$$$\:\:{x}_{\mathrm{2}} =\mathrm{1} \\ $$$${when}\:{n}=\mathrm{2} \\ $$$$\:\:{x}_{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${when}\:{n}=\mathrm{3} \\ $$$$\:\:{x}_{\mathrm{4}} =\mathrm{2}\sqrt{\mathrm{2}}\sqrt{\mathrm{2}}+\sqrt{\mathrm{8}+\mathrm{1}}=\mathrm{7} \\ $$$$… \\ $$$${when}\:{n}>\mathrm{2}\:\:\:\:\:{x}_{{n}} ,{x}_{{n}−\mathrm{1}} >\mathrm{1} \\ $$$${x}_{{n}+\mathrm{1}} ={x}_{{n}} \sqrt{{x}_{{n}−\mathrm{1}} ^{\mathrm{2}} +\mathrm{1}}+{x}_{{n}−\mathrm{1}} \sqrt{{x}_{{n}} ^{\mathrm{2}} +\mathrm{1}}\centerdot\centerdot\centerdot\left(\ast\right) \\ $$$${x}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}} −\frac{\mathrm{1}}{{y}_{{n}} }\right)\left({y}_{{n}} \geqslant\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}+\mathrm{1}} −{y}_{{n}+\mathrm{1}} ^{−\mathrm{1}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}} −{y}_{{n}} ^{−\mathrm{1}} \right)\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}−\mathrm{1}} +{y}_{{n}−\mathrm{1}} ^{−\mathrm{1}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}−\mathrm{1}} −{y}_{{n}−\mathrm{1}} ^{−\mathrm{1}} \right)\frac{\mathrm{1}}{\mathrm{2}}\left({y}_{{n}} +{y}_{{n}} ^{−\mathrm{1}} \right) \\ $$$$\mathrm{2}\left({y}_{{n}+\mathrm{1}} −{y}_{{n}+\mathrm{1}} ^{−\mathrm{1}} \right)=\left({y}_{{n}} −{y}_{{n}} ^{−\mathrm{1}} \right)\left({y}_{{n}−\mathrm{1}} +{y}_{{n}−\mathrm{1}} ^{−\mathrm{1}} \right)+\left({y}_{{n}−\mathrm{1}} −{y}_{{n}−\mathrm{1}} ^{−\mathrm{1}} \right)\left({y}_{{n}} +{y}_{{n}} ^{−\mathrm{1}} \right) \\ $$$$\mathrm{2}\left({y}_{{n}+\mathrm{1}} −{y}_{{n}+\mathrm{1}} ^{−\mathrm{1}} \right)=\mathrm{2}{y}_{{n}} {y}_{{n}−\mathrm{1}} −\mathrm{2}{y}_{{n}} ^{−\mathrm{1}} {y}_{{n}} ^{−\mathrm{1}} \\ $$$${y}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{{y}_{{n}+\mathrm{1}} }={y}_{{n}} {y}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{{y}_{{n}} {y}_{{n}−\mathrm{1}} } \\ $$$${y}_{{n}+\mathrm{1}} ^{\mathrm{2}} −\left({y}_{{n}} {y}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{{y}_{{n}} {y}_{{n}−\mathrm{1}} }\right){y}_{{n}+\mathrm{1}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({y}_{{n}+\mathrm{1}} −{y}_{{n}} {y}_{{n}−\mathrm{1}} \right)\left({y}_{{n}+\mathrm{1}} +\frac{\mathrm{1}}{{y}_{{n}} {y}_{{n}−\mathrm{1}} }\right)=\mathrm{0} \\ $$$${y}_{{n}+\mathrm{1}} ={y}_{{n}} {y}_{{n}−\mathrm{1}} \left(\because{y}_{{n}} >\mathrm{0}\right) \\ $$$$ \\ $$$${x}_{\mathrm{0}} =\mathrm{0},{y}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{0}{y}_{\mathrm{0}} −\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:{y}_{\mathrm{0}} =\mathrm{1} \\ $$$${x}_{\mathrm{1}} =\mathrm{1},{y}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{y}_{\mathrm{1}} −\mathrm{1}=\mathrm{0} \\ $$$$\:\:{y}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$${y}_{{n}} ={y}_{{n}−\mathrm{1}} {y}_{{n}−\mathrm{2}} ={y}_{{n}−\mathrm{2}} ^{\mathrm{2}} {y}_{{n}−\mathrm{3}} ={y}_{{n}−\mathrm{3}} ^{\mathrm{3}} {y}_{{n}−\mathrm{4}} ^{\mathrm{2}} ={y}_{{n}−\mathrm{4}} ^{\mathrm{5}} {y}_{{n}−\mathrm{5}} ^{\mathrm{3}} =… \\ $$$${y}_{\mathrm{2}} =\mathrm{1}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right),{y}_{\mathrm{3}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ,{y}_{\mathrm{4}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{3}} ,{y}_{\mathrm{5}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{5}} … \\ $$$$\mathrm{1}\:\mathrm{1}\:\mathrm{2}\:\mathrm{3}\:\mathrm{5}\:\mathrm{8}\:\mathrm{13}\:\mathrm{21}…{fibonacci} \\ $$$${y}_{{n}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{f}\left({n}\right)} \:\:\:\begin{cases}{{f}\left({n}\right)={f}\left({n}−\mathrm{1}\right)+{f}\left({n}−\mathrm{2}\right)}\\{{f}\left(\mathrm{0}\right)=\mathrm{0},{f}\left(\mathrm{1}\right)=\mathrm{1}}\end{cases} \\ $$$${f}\left({n}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right\} \\ $$$$\:\:\:\:\:=\frac{\phi^{{n}} −\left(−\phi\right)^{−{n}} }{\:\sqrt{\mathrm{5}}},\left(\phi=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$$${x}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{f}\left({n}\right)} −\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−{f}\left({n}\right)} \right\} \\ $$$$++++++++++++ \\ $$$${x}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{0}} −\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{0}} \right\}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}+\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right\}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}=\mathrm{1} \\ $$$${x}_{\mathrm{2}} ={x}_{\mathrm{1}} =\mathrm{1} \\ $$$${x}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\right\}=\frac{\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right)\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\left(\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right)\left(\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right)}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$… \\ $$
Commented by sou1618 last updated on 03/Sep/16
if you need fibonacci=f(n) a_0 =0,a_1 =1 a_n =a_(n−1) +a_(n−2) (n≥2) a_n −pa_(n−1) =q(a_(n−1) −pa_(n−2) ) a_n =(p+q)a_(n−1) −pqa_(n−2) { ((p+q=1)),((pq=−1)) :} p^2 −p+p=0 p=((1±(√5))/2) (p,q)=(((1+(√5))/2),((1−(√5))/2)) { ((a_n −pa_(n−1) =q(a_(n−1) −pa_(n−2) ))),((a_n −qa_(n−1) =p(a_(n−1) −qa_(n−2) ))) :} when n=2 { ((a_1 −pa_0 =1)),((a_1 −qa_0 =1)) :} so { ((a_n −pa_(n−1) =q^(n−1) ∙∙∙(1))),((a_n −qa_(n−1) =p^(n−1) ∙∙∙(2))) :} (2)−(1)⇒ (p−q)a_(n−1) =p^(n−1) −q^(n−1) a_n =(1/(p−q))(p^n −q^n ) a_n =(1/( (√5))){(((1+(√5))/2))^n −(((1−(√5))/2))^n } f(n)=a_n
$${if}\:{you}\:{need}\:{fibonacci}={f}\left({n}\right) \\ $$$${a}_{\mathrm{0}} =\mathrm{0},{a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +{a}_{{n}−\mathrm{2}} \left({n}\geqslant\mathrm{2}\right) \\ $$$${a}_{{n}} −{pa}_{{n}−\mathrm{1}} ={q}\left({a}_{{n}−\mathrm{1}} −{pa}_{{n}−\mathrm{2}} \right) \\ $$$${a}_{{n}} =\left({p}+{q}\right){a}_{{n}−\mathrm{1}} −{pqa}_{{n}−\mathrm{2}} \\ $$$$\begin{cases}{{p}+{q}=\mathrm{1}}\\{{pq}=−\mathrm{1}}\end{cases} \\ $$$${p}^{\mathrm{2}} −{p}+{p}=\mathrm{0} \\ $$$${p}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\left({p},{q}\right)=\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\begin{cases}{{a}_{{n}} −{pa}_{{n}−\mathrm{1}} ={q}\left({a}_{{n}−\mathrm{1}} −{pa}_{{n}−\mathrm{2}} \right)}\\{{a}_{{n}} −{qa}_{{n}−\mathrm{1}} ={p}\left({a}_{{n}−\mathrm{1}} −{qa}_{{n}−\mathrm{2}} \right)}\end{cases} \\ $$$${when}\:{n}=\mathrm{2} \\ $$$$\begin{cases}{{a}_{\mathrm{1}} −{pa}_{\mathrm{0}} =\mathrm{1}}\\{{a}_{\mathrm{1}} −{qa}_{\mathrm{0}} =\mathrm{1}}\end{cases} \\ $$$${so} \\ $$$$\begin{cases}{{a}_{{n}} −{pa}_{{n}−\mathrm{1}} ={q}^{{n}−\mathrm{1}} \centerdot\centerdot\centerdot\left(\mathrm{1}\right)}\\{{a}_{{n}} −{qa}_{{n}−\mathrm{1}} ={p}^{{n}−\mathrm{1}} \centerdot\centerdot\centerdot\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\Rightarrow \\ $$$$\left({p}−{q}\right){a}_{{n}−\mathrm{1}} ={p}^{{n}−\mathrm{1}} −{q}^{{n}−\mathrm{1}} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{{p}−{q}}\left({p}^{{n}} −{q}^{{n}} \right) \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right\} \\ $$$$ \\ $$$${f}\left({n}\right)={a}_{{n}} \\ $$
Commented by Yozzia last updated on 03/Sep/16
Nicely! What if you let x_n =sinh{u(n)} initially?
$${Nicely}!\:{What}\:{if}\:{you}\:{let}\:{x}_{{n}} ={sinh}\left\{{u}\left({n}\right)\right\}\:{initially}? \\ $$$$ \\ $$$$ \\ $$
Commented by sou1618 last updated on 03/Sep/16
it′s nice idea!! x_n =sinh(u_n ) sinh(u_(n+1) )=sinh(u_n )cosh(u_(n−1) )+sinh(u_(n−1) )cosh(u_n ) sinh(u_(n+1) )=sinh(u_n +u_(n−1) ) u_(n+1) =u_n +u_(n−1) u_0 =0 u_1 =ln(1+(√2)) so u_n =ln(1+(√2))×f(n) x_n =sinh{ln(1+(√2))f(n)} =(1/2){(1+(√2))^(f(n)) −(1+(√2))^(−f(n)) }
$${it}'{s}\:{nice}\:{idea}!! \\ $$$${x}_{{n}} ={sinh}\left({u}_{{n}} \right) \\ $$$${sinh}\left({u}_{{n}+\mathrm{1}} \right)={sinh}\left({u}_{{n}} \right){cosh}\left({u}_{{n}−\mathrm{1}} \right)+{sinh}\left({u}_{{n}−\mathrm{1}} \right){cosh}\left({u}_{{n}} \right) \\ $$$${sinh}\left({u}_{{n}+\mathrm{1}} \right)={sinh}\left({u}_{{n}} +{u}_{{n}−\mathrm{1}} \right) \\ $$$${u}_{{n}+\mathrm{1}} ={u}_{{n}} +{u}_{{n}−\mathrm{1}} \\ $$$${u}_{\mathrm{0}} =\mathrm{0} \\ $$$${u}_{\mathrm{1}} ={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${so} \\ $$$${u}_{{n}} ={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)×{f}\left({n}\right) \\ $$$$ \\ $$$${x}_{{n}} ={sinh}\left\{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){f}\left({n}\right)\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{f}\left({n}\right)} −\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−{f}\left({n}\right)} \right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *