Question Number 74346 by mathmax by abdo last updated on 22/Nov/19
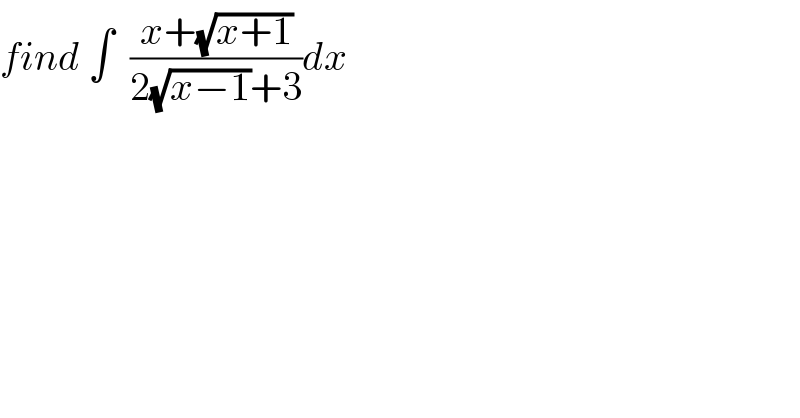
$${find}\:\int\:\:\frac{{x}+\sqrt{{x}+\mathrm{1}}}{\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{3}}{dx} \\ $$
Answered by MJS last updated on 24/Nov/19
![∫((x+(√(x+1)))/(3+2(√(x−1))))dx= [t=2(√(x−1)) → dx=(√(x−1))dt] =(1/4)∫((t(√(t^2 +8)))/(t+3))dt+(1/8)∫t^2 dt−(3/8)∫tdt+((13)/8)∫dt−((39)/8)∫(dt/(t+3))= =(1/4)∫((t(√(t^2 +8)))/(t+3))dt+(1/(24))t^3 −(3/(16))t^2 +((13)/8)t−((39)/8)ln (t+3) ∫((t(√(t^2 +8)))/(t+3))dt= [u=((√2)/4)(t+(√(t^2 +8))) → dt=((2(√(2(t^2 +8))))/(t+(√(t^2 +8))))du] =−((51(√2))/8)∫(du/(u^2 +((3(√2))/2)u−1))+(1/2)∫udu−((3(√2))/4)∫du+((13)/4)∫(du/u)+((3(√2))/4)∫(du/u^2 )+(1/2)∫(du/u^3 )= =((3(√(17)))/4)ln ((4u+(3+(√(17)))(√2))/(4u+(3−(√(17)))(√2))) +(1/4)u^2 −((3(√2))/4)u+((13)/4)ln u −((3(√2))/(4u))−(1/(4u^2 ))= ... now just insert the substitutions](https://www.tinkutara.com/question/Q74407.png)
$$\int\frac{{x}+\sqrt{{x}+\mathrm{1}}}{\mathrm{3}+\mathrm{2}\sqrt{{x}−\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}\sqrt{{x}−\mathrm{1}}\:\rightarrow\:{dx}=\sqrt{{x}−\mathrm{1}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{8}}}{{t}+\mathrm{3}}{dt}+\frac{\mathrm{1}}{\mathrm{8}}\int{t}^{\mathrm{2}} {dt}−\frac{\mathrm{3}}{\mathrm{8}}\int{tdt}+\frac{\mathrm{13}}{\mathrm{8}}\int{dt}−\frac{\mathrm{39}}{\mathrm{8}}\int\frac{{dt}}{{t}+\mathrm{3}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{8}}}{{t}+\mathrm{3}}{dt}+\frac{\mathrm{1}}{\mathrm{24}}{t}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{16}}{t}^{\mathrm{2}} +\frac{\mathrm{13}}{\mathrm{8}}{t}−\frac{\mathrm{39}}{\mathrm{8}}\mathrm{ln}\:\left({t}+\mathrm{3}\right) \\ $$$$ \\ $$$$\int\frac{{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{8}}}{{t}+\mathrm{3}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{8}}\right)\:\rightarrow\:{dt}=\frac{\mathrm{2}\sqrt{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{8}\right)}}{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{8}}}{du}\right] \\ $$$$=−\frac{\mathrm{51}\sqrt{\mathrm{2}}}{\mathrm{8}}\int\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}{u}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int{udu}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\int{du}+\frac{\mathrm{13}}{\mathrm{4}}\int\frac{{du}}{{u}}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{du}}{{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}^{\mathrm{3}} }= \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{4}{u}+\left(\mathrm{3}+\sqrt{\mathrm{17}}\right)\sqrt{\mathrm{2}}}{\mathrm{4}{u}+\left(\mathrm{3}−\sqrt{\mathrm{17}}\right)\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\mathrm{4}}{u}^{\mathrm{2}} −\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}{u}+\frac{\mathrm{13}}{\mathrm{4}}\mathrm{ln}\:{u}\:−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}{u}}−\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{2}} }= \\ $$$$… \\ $$$$\mathrm{now}\:\mathrm{just}\:\mathrm{insert}\:\mathrm{the}\:\mathrm{substitutions} \\ $$
Commented by abdomathmax last updated on 24/Nov/19

$${thankx}\:{sir}\:{mjs}. \\ $$
