Question Number 137004 by Mathspace last updated on 28/Mar/21
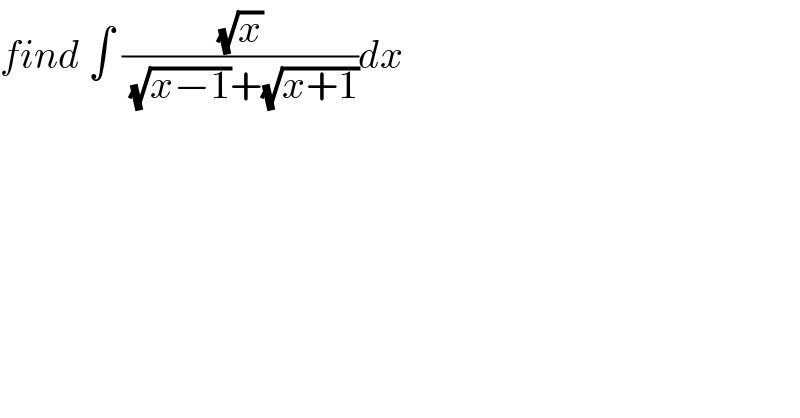
$${find}\:\int\:\frac{\sqrt{{x}}}{\:\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}}{dx} \\ $$
Answered by aleks041103 last updated on 28/Mar/21
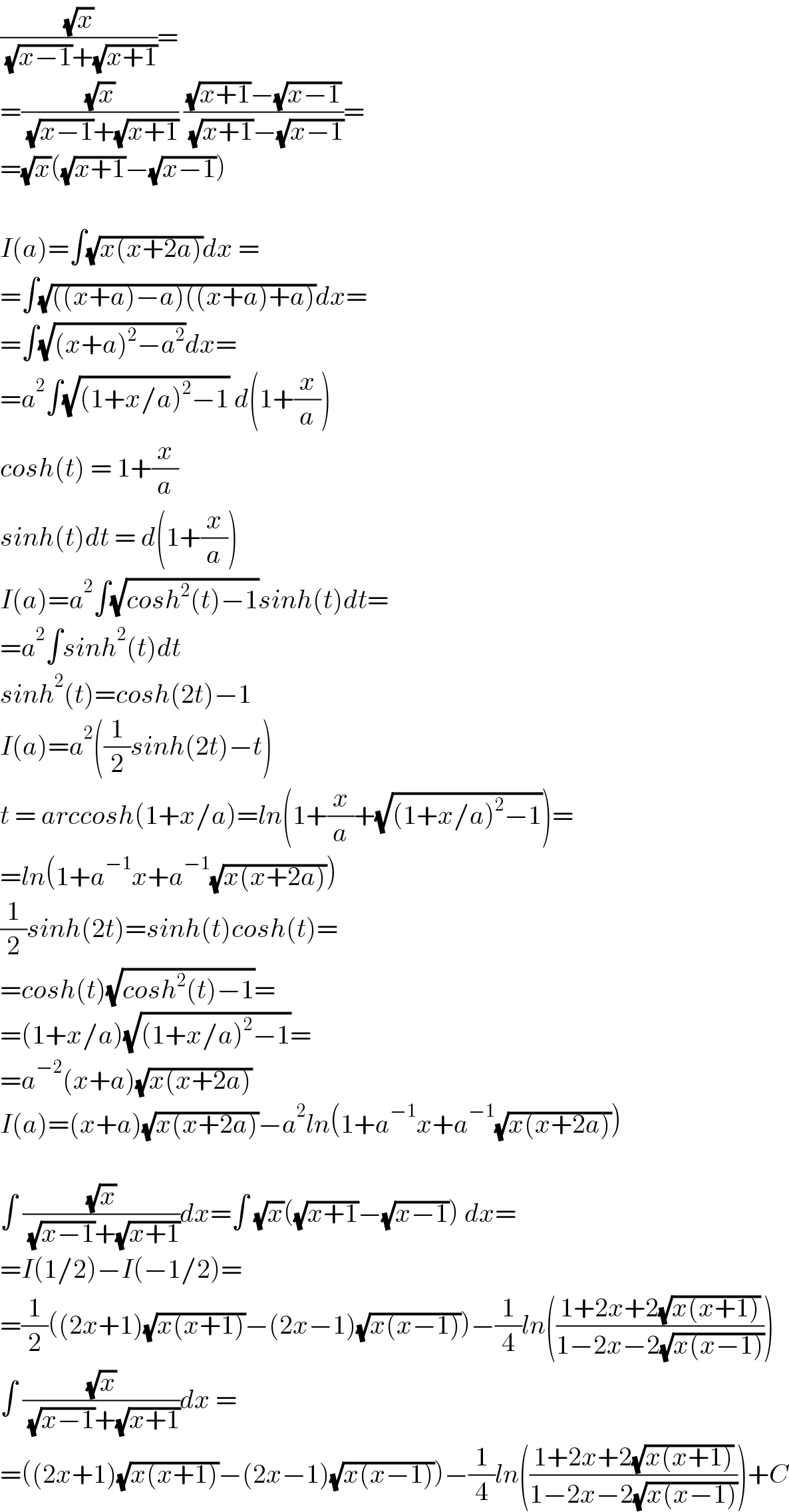
$$\frac{\sqrt{{x}}}{\:\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}}= \\ $$$$=\frac{\sqrt{{x}}}{\:\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}}\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}= \\ $$$$=\sqrt{{x}}\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\right) \\ $$$$ \\ $$$${I}\left({a}\right)=\int\sqrt{{x}\left({x}+\mathrm{2}{a}\right)}{dx}\:=\: \\ $$$$=\int\sqrt{\left(\left({x}+{a}\right)−{a}\right)\left(\left({x}+{a}\right)+{a}\right)}{dx}= \\ $$$$=\int\sqrt{\left({x}+{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}= \\ $$$$={a}^{\mathrm{2}} \int\sqrt{\left(\mathrm{1}+{x}/{a}\right)^{\mathrm{2}} −\mathrm{1}}\:{d}\left(\mathrm{1}+\frac{{x}}{{a}}\right) \\ $$$${cosh}\left({t}\right)\:=\:\mathrm{1}+\frac{{x}}{{a}} \\ $$$${sinh}\left({t}\right){dt}\:=\:{d}\left(\mathrm{1}+\frac{{x}}{{a}}\right) \\ $$$${I}\left({a}\right)={a}^{\mathrm{2}} \int\sqrt{{cosh}^{\mathrm{2}} \left({t}\right)−\mathrm{1}}{sinh}\left({t}\right){dt}= \\ $$$$={a}^{\mathrm{2}} \int{sinh}^{\mathrm{2}} \left({t}\right){dt} \\ $$$${sinh}^{\mathrm{2}} \left({t}\right)={cosh}\left(\mathrm{2}{t}\right)−\mathrm{1} \\ $$$${I}\left({a}\right)={a}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{sinh}\left(\mathrm{2}{t}\right)−{t}\right) \\ $$$${t}\:=\:{arccosh}\left(\mathrm{1}+{x}/{a}\right)={ln}\left(\mathrm{1}+\frac{{x}}{{a}}+\sqrt{\left(\mathrm{1}+{x}/{a}\right)^{\mathrm{2}} −\mathrm{1}}\right)= \\ $$$$={ln}\left(\mathrm{1}+{a}^{−\mathrm{1}} {x}+{a}^{−\mathrm{1}} \sqrt{{x}\left({x}+\mathrm{2}{a}\right)}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{sinh}\left(\mathrm{2}{t}\right)={sinh}\left({t}\right){cosh}\left({t}\right)= \\ $$$$={cosh}\left({t}\right)\sqrt{{cosh}^{\mathrm{2}} \left({t}\right)−\mathrm{1}}= \\ $$$$=\left(\mathrm{1}+{x}/{a}\right)\sqrt{\left(\mathrm{1}+{x}/{a}\right)^{\mathrm{2}} −\mathrm{1}}= \\ $$$$={a}^{−\mathrm{2}} \left({x}+{a}\right)\sqrt{{x}\left({x}+\mathrm{2}{a}\right)} \\ $$$${I}\left({a}\right)=\left({x}+{a}\right)\sqrt{{x}\left({x}+\mathrm{2}{a}\right)}−{a}^{\mathrm{2}} {ln}\left(\mathrm{1}+{a}^{−\mathrm{1}} {x}+{a}^{−\mathrm{1}} \sqrt{{x}\left({x}+\mathrm{2}{a}\right)}\right) \\ $$$$ \\ $$$$\int\:\frac{\sqrt{{x}}}{\:\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}}{dx}=\int\:\sqrt{{x}}\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\right)\:{dx}= \\ $$$$={I}\left(\mathrm{1}/\mathrm{2}\right)−{I}\left(−\mathrm{1}/\mathrm{2}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}\left({x}+\mathrm{1}\right)}−\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}\left({x}−\mathrm{1}\right)}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\mathrm{2}{x}+\mathrm{2}\sqrt{{x}\left({x}+\mathrm{1}\right)}}{\mathrm{1}−\mathrm{2}{x}−\mathrm{2}\sqrt{{x}\left({x}−\mathrm{1}\right)}}\right) \\ $$$$\int\:\frac{\sqrt{{x}}}{\:\sqrt{{x}−\mathrm{1}}+\sqrt{{x}+\mathrm{1}}}{dx}\:= \\ $$$$=\left(\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}\left({x}+\mathrm{1}\right)}−\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}\left({x}−\mathrm{1}\right)}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\mathrm{2}{x}+\mathrm{2}\sqrt{{x}\left({x}+\mathrm{1}\right)}}{\mathrm{1}−\mathrm{2}{x}−\mathrm{2}\sqrt{{x}\left({x}−\mathrm{1}\right)}}\right)+{C} \\ $$
Answered by mathmax by abdo last updated on 29/Mar/21

$$\mathrm{thankx}\:\mathrm{sir}. \\ $$
Answered by EDWIN88 last updated on 29/Mar/21
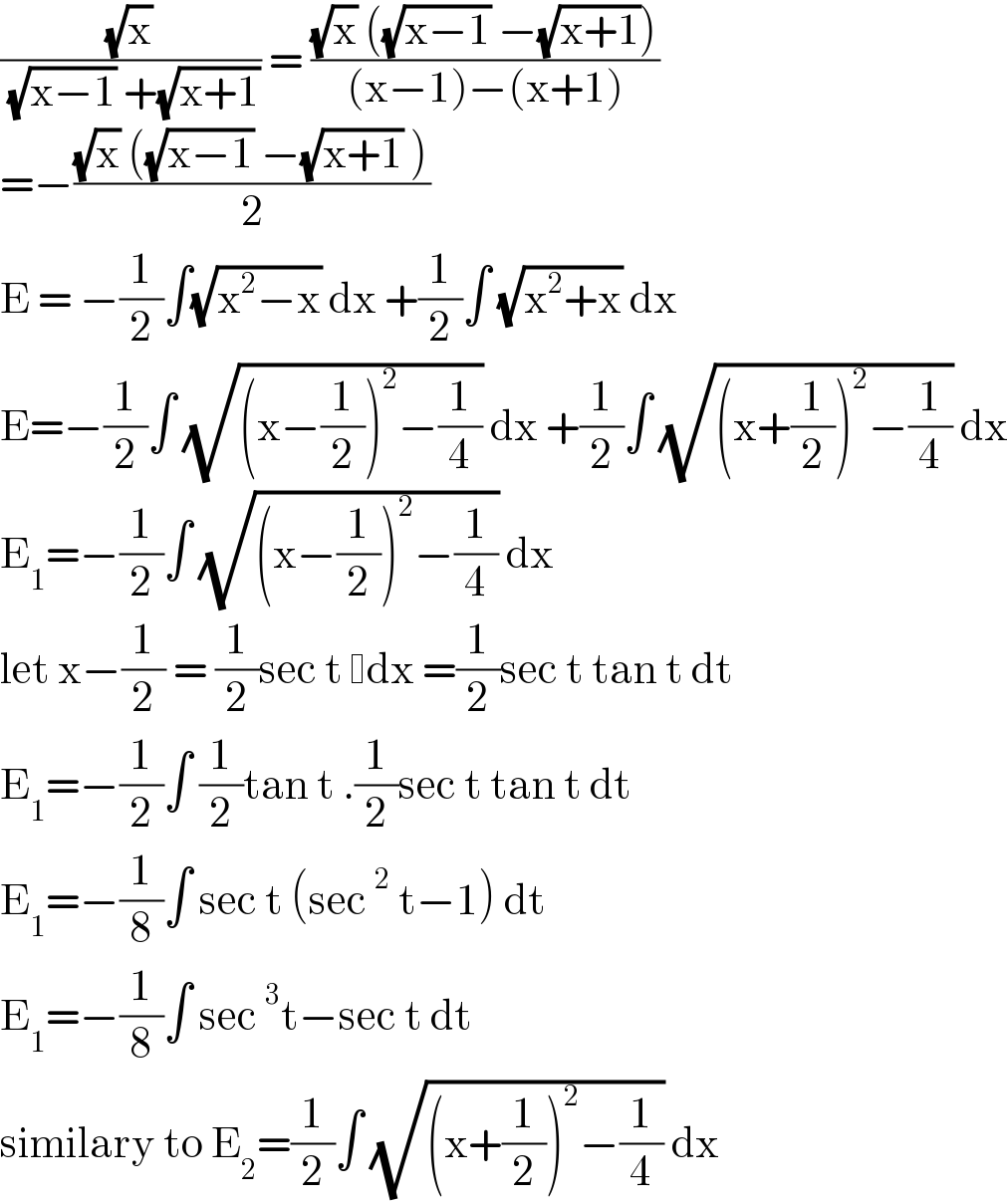
$$\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}−\mathrm{1}}\:+\sqrt{\mathrm{x}+\mathrm{1}}}\:=\:\frac{\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}−\mathrm{1}}\:−\sqrt{\mathrm{x}+\mathrm{1}}\right)}{\left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{x}+\mathrm{1}\right)} \\ $$$$=−\frac{\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}−\mathrm{1}}\:−\sqrt{\mathrm{x}+\mathrm{1}}\:\right)}{\mathrm{2}} \\ $$$$\mathrm{E}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}}\:\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{E}=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:\mathrm{dx} \\ $$$$\mathrm{E}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\: \mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{E}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\mathrm{t}\:.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{E}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{8}}\int\:\mathrm{sec}\:\mathrm{t}\:\left(\mathrm{sec}\:^{\mathrm{2}} \:\mathrm{t}−\mathrm{1}\right)\:\mathrm{dt}\: \\ $$$$\mathrm{E}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{8}}\int\:\mathrm{sec}\:^{\mathrm{3}} \mathrm{t}−\mathrm{sec}\:\mathrm{t}\:\mathrm{dt}\: \\ $$$$\mathrm{similary}\:\mathrm{to}\:\mathrm{E}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}\:\mathrm{dx} \\ $$
