Question Number 8488 by Basant007 last updated on 12/Oct/16
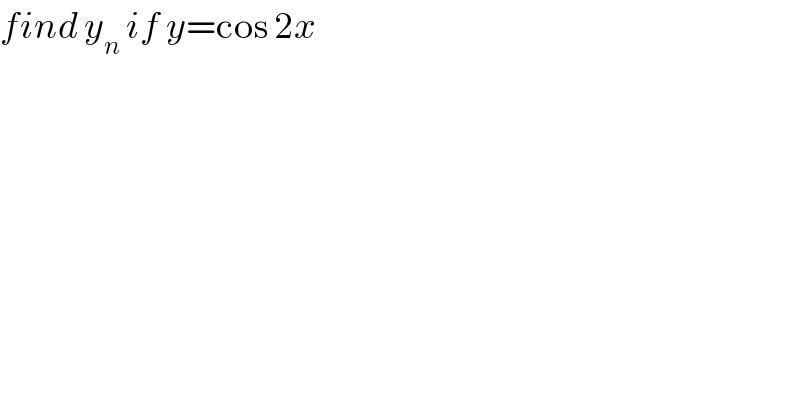
$${find}\:{y}_{{n}} \:{if}\:{y}=\mathrm{cos}\:\mathrm{2}{x} \\ $$
Commented by FilupSmith last updated on 13/Oct/16
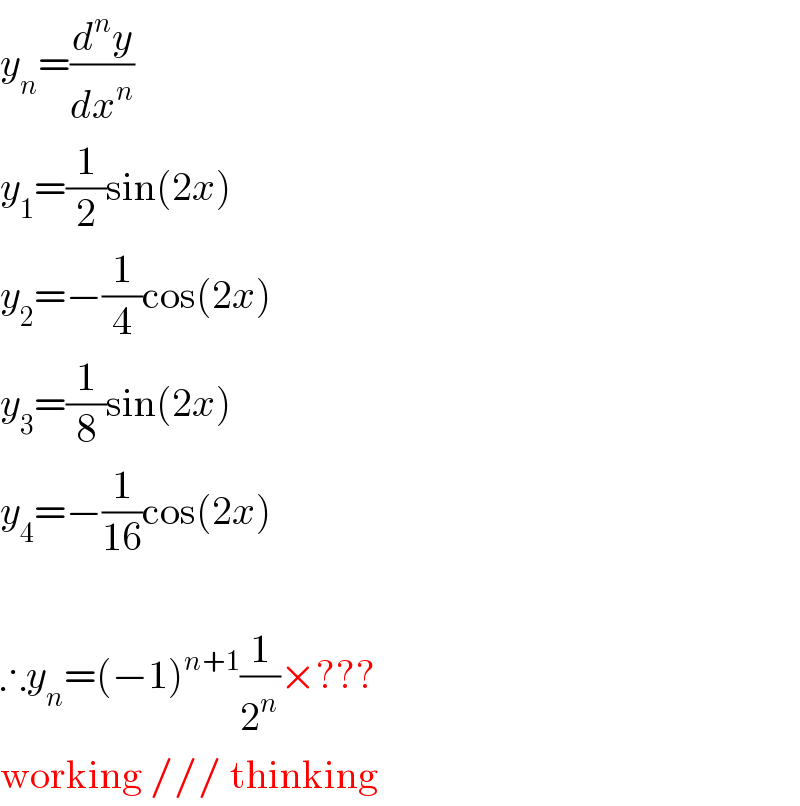
$${y}_{{n}} =\frac{{d}^{{n}} {y}}{{dx}^{{n}} } \\ $$$${y}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$${y}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\mathrm{2}{x}\right) \\ $$$${y}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$${y}_{\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos}\left(\mathrm{2}{x}\right) \\ $$$$\: \\ $$$$\therefore{y}_{{n}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}^{{n}} }×??? \\ $$$$\mathrm{working}\:///\:\mathrm{thinking} \\ $$
Commented by Rasheed Soomro last updated on 13/Oct/16
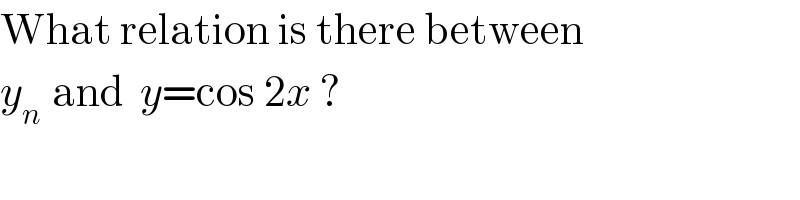
$$\mathrm{What}\:\mathrm{relation}\:\mathrm{is}\:\mathrm{there}\:\mathrm{between} \\ $$$${y}_{{n}\:\:} \mathrm{and}\:\:{y}=\mathrm{cos}\:\mathrm{2}{x}\:? \\ $$
Commented by Basant007 last updated on 13/Oct/16
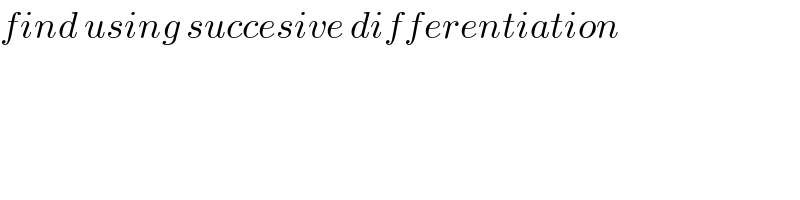
$${find}\:{using}\:{succesive}\:{differentiation} \\ $$
Commented by Basant007 last updated on 13/Oct/16

$${i}.{e}\:{y}_{{n}} \\ $$
Commented by FilupSmith last updated on 13/Oct/16
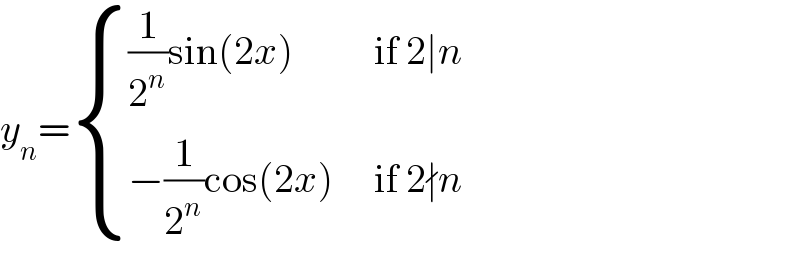
$${y}_{{n}} =\begin{cases}{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\mathrm{sin}\left(\mathrm{2}{x}\right)\:\:\:\:\:\:\:\:\:\:\mathrm{if}\:\mathrm{2}\mid{n}}\\{−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\mathrm{cos}\left(\mathrm{2}{x}\right)\:\:\:\:\:\mathrm{if}\:\mathrm{2}\nmid{n}}\end{cases} \\ $$
Commented by Basant007 last updated on 13/Oct/16
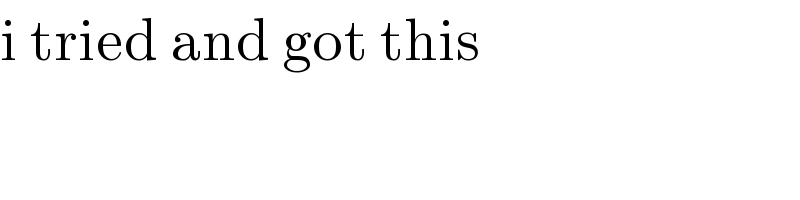
$$\mathrm{i}\:\mathrm{tried}\:\mathrm{and}\:\mathrm{got}\:\mathrm{this} \\ $$
Commented by Basant007 last updated on 13/Oct/16
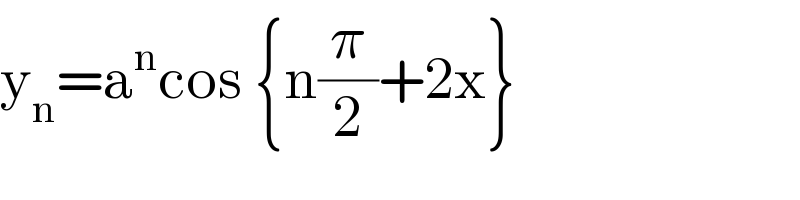
$$\mathrm{y}_{\mathrm{n}} =\mathrm{a}^{\mathrm{n}} \mathrm{cos}\:\left\{\mathrm{n}\frac{\pi}{\mathrm{2}}+\mathrm{2x}\right\} \\ $$
