Question Number 74350 by mathmax by abdo last updated on 22/Nov/19

$${findf}\left({a}\right)=\:\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({cosx}\right)}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}\:{witha}>\mathrm{0} \\ $$
Commented by abdomathmax last updated on 23/Nov/19
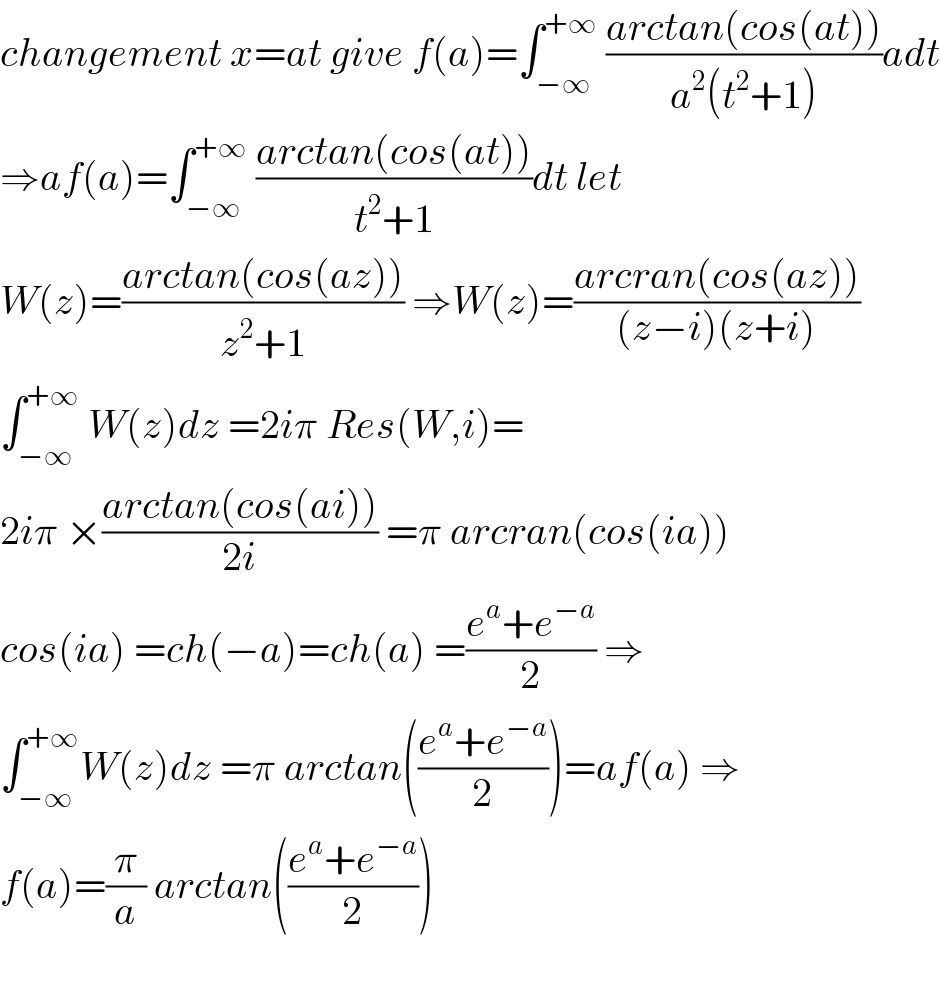
$${changement}\:{x}={at}\:{give}\:{f}\left({a}\right)=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({cos}\left({at}\right)\right)}{{a}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)}{adt} \\ $$$$\Rightarrow{af}\left({a}\right)=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({cos}\left({at}\right)\right)}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:{let}\: \\ $$$${W}\left({z}\right)=\frac{{arctan}\left({cos}\left({az}\right)\right)}{{z}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow{W}\left({z}\right)=\frac{{arcran}\left({cos}\left({az}\right)\right)}{\left({z}−{i}\right)\left({z}+{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{i}\right)= \\ $$$$\mathrm{2}{i}\pi\:×\frac{{arctan}\left({cos}\left({ai}\right)\right)}{\mathrm{2}{i}}\:=\pi\:{arcran}\left({cos}\left({ia}\right)\right) \\ $$$${cos}\left({ia}\right)\:={ch}\left(−{a}\right)={ch}\left({a}\right)\:=\frac{{e}^{{a}} +{e}^{−{a}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\:=\pi\:{arctan}\left(\frac{{e}^{{a}} +{e}^{−{a}} }{\mathrm{2}}\right)={af}\left({a}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)=\frac{\pi}{{a}}\:{arctan}\left(\frac{{e}^{{a}} +{e}^{−{a}} }{\mathrm{2}}\right) \\ $$$$ \\ $$
