Question Number 72824 by Rio Michael last updated on 03/Nov/19
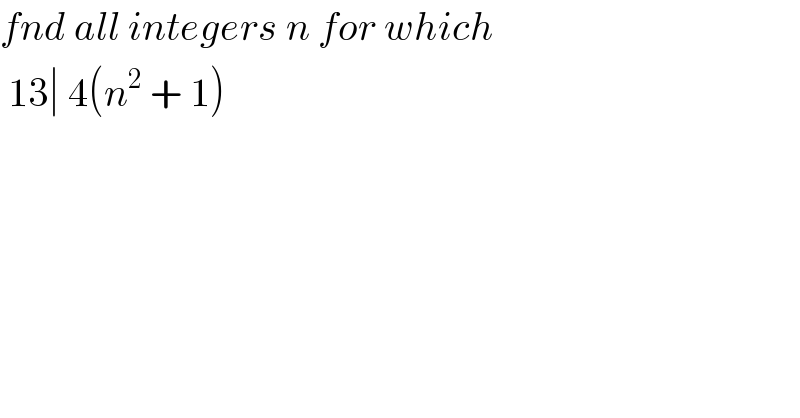
$${fnd}\:{all}\:{integers}\:{n}\:{for}\:{which}\: \\ $$$$\:\mathrm{13}\mid\:\mathrm{4}\left({n}^{\mathrm{2}} \:+\:\mathrm{1}\right) \\ $$
Answered by mind is power last updated on 03/Nov/19
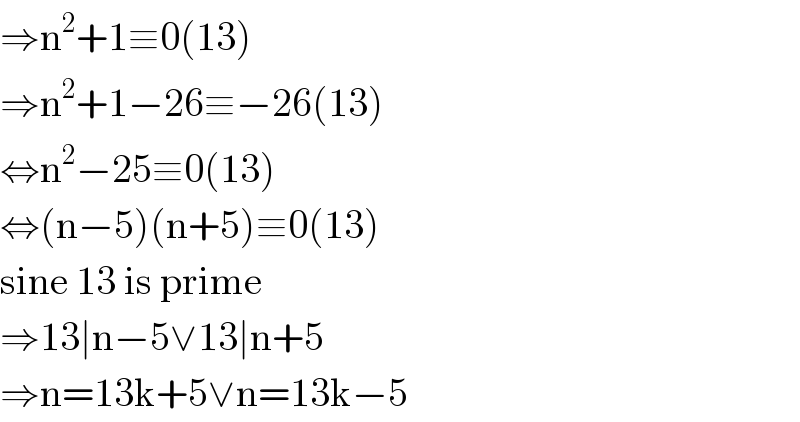
$$\Rightarrow\mathrm{n}^{\mathrm{2}} +\mathrm{1}\equiv\mathrm{0}\left(\mathrm{13}\right) \\ $$$$\Rightarrow\mathrm{n}^{\mathrm{2}} +\mathrm{1}−\mathrm{26}\equiv−\mathrm{26}\left(\mathrm{13}\right) \\ $$$$\Leftrightarrow\mathrm{n}^{\mathrm{2}} −\mathrm{25}\equiv\mathrm{0}\left(\mathrm{13}\right) \\ $$$$\Leftrightarrow\left(\mathrm{n}−\mathrm{5}\right)\left(\mathrm{n}+\mathrm{5}\right)\equiv\mathrm{0}\left(\mathrm{13}\right) \\ $$$$\mathrm{sine}\:\mathrm{13}\:\mathrm{is}\:\mathrm{prime} \\ $$$$\Rightarrow\mathrm{13}\mid\mathrm{n}−\mathrm{5}\vee\mathrm{13}\mid\mathrm{n}+\mathrm{5} \\ $$$$\Rightarrow\mathrm{n}=\mathrm{13k}+\mathrm{5}\vee\mathrm{n}=\mathrm{13k}−\mathrm{5} \\ $$
Commented by Rio Michael last updated on 03/Nov/19
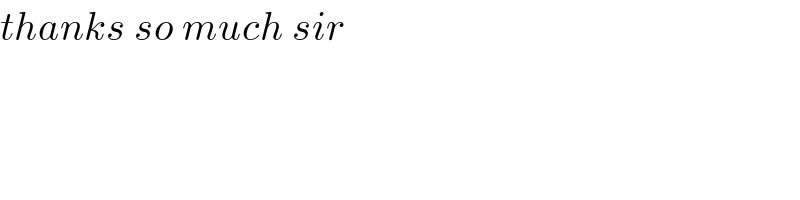
$${thanks}\:{so}\:{much}\:{sir} \\ $$
