Question Number 4752 by Yozzii last updated on 04/Mar/16
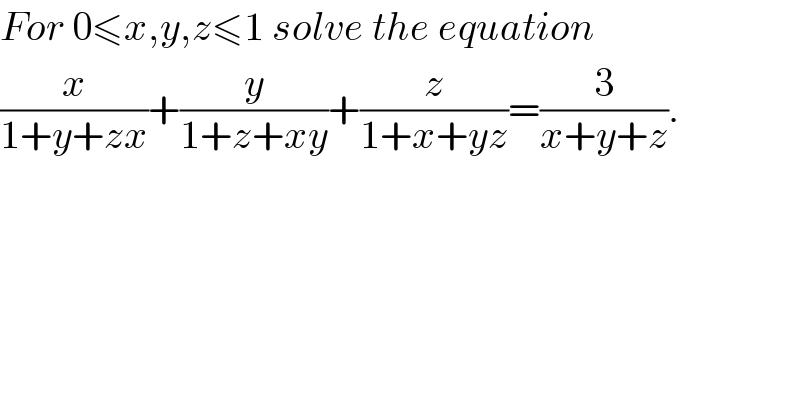
$${For}\:\mathrm{0}\leqslant{x},{y},{z}\leqslant\mathrm{1}\:{solve}\:{the}\:{equation} \\ $$$$\frac{{x}}{\mathrm{1}+{y}+{zx}}+\frac{{y}}{\mathrm{1}+{z}+{xy}}+\frac{{z}}{\mathrm{1}+{x}+{yz}}=\frac{\mathrm{3}}{{x}+{y}+{z}}. \\ $$
Commented by prakash jain last updated on 05/Mar/16
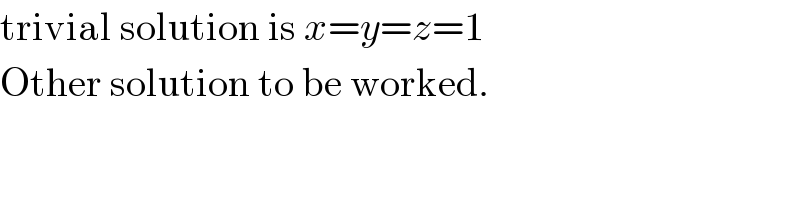
$$\mathrm{trivial}\:\mathrm{solution}\:\mathrm{is}\:{x}={y}={z}=\mathrm{1} \\ $$$$\mathrm{Other}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{be}\:\mathrm{worked}. \\ $$
