Menu Close

for-a-gt-0-and-b-gt-a-2-verify-the-follwing-claim-n-1-n-a-a-1-a-2-a-n-1-b-b-1-b-2-b-n-1-a-b-1-b-a-1-b-a-2-

Tinku Tara 0 Comments
Pin




Question Number 78456 by arkanmath7@gmail.com last updated on 17/Jan/20
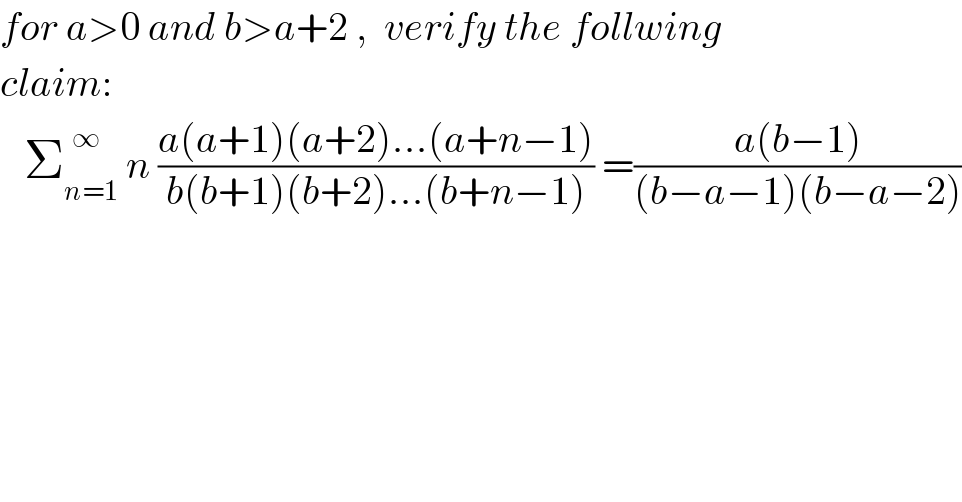
for a>0 and b>a+2 , verify the follwing claim: Σ_(n=1) ^( ∞) n ((a(a+1)(a+2)...(a+n−1))/(b(b+1)(b+2)...(b+n−1))) =((a(b−1))/((b−a−1)(b−a−2)))
$${for}\:{a}>\mathrm{0}\:{and}\:{b}>{a}+\mathrm{2}\:,\:\:{verify}\:{the}\:{follwing}\: \\ $$$${claim}: \\ $$$$\:\:\:\sum_{{n}=\mathrm{1}} ^{\:\:\infty} \:{n}\:\frac{{a}\left({a}+\mathrm{1}\right)\left({a}+\mathrm{2}\right)…\left({a}+{n}−\mathrm{1}\right)}{{b}\left({b}+\mathrm{1}\right)\left({b}+\mathrm{2}\right)…\left({b}+{n}−\mathrm{1}\right)}\:=\frac{{a}\left({b}−\mathrm{1}\right)}{\left({b}−{a}−\mathrm{1}\right)\left({b}−{a}−\mathrm{2}\right)} \\ $$
Answered by mind is power last updated on 17/Jan/20
=Σ_(n≥1) (((n+1−1)a_n )/b_n )=Σ_(n≥1) (((n+1)!.a_n )/(b_n .n!))−Σ_(n≥1) ((n!.a_n )/(n!.b_n ))=S a_n =a(a+1)...(a+n−1) _2 F_1 (a,b,c,z)=1+Σ_(n≥1) ((a_n .b_n )/c_n ).(z^n /(n!)) = lim_(z→1) { _2 F_1 (a,2,b,z)−_2 F_1 (a,1,b,z)} we have β(b,c−b).2F_1 (a,b,c,z)=∫_0 ^1 x^(b−1) (1−x)^(c−b−1) (1−zx)^(−a) dx β(b,c−b) _2 F_1 (a,b,c,1)=∫_0 ^1 x^(b−1) (1−x)^(c−b−a−1) dx ⇒β(b,c−b) _2 F_1 (a,b,c,1)=β(b,c−b−a) ⇒_2 F_1 =((β(b,c−b−a))/(β(b,c−b)))=((Γ(b)Γ(c−b−a)Γ(c))/(Γ(c−a)Γ(b)Γ(c−b)))⇔ 2F_1 (a,b,c,1)=((Γ(c).Γ(c−a−b))/(Γ(c−a)Γ(c−b))) 2F_1 (a,2,b,1)=((Γ(b)Γ(b−a−2))/(Γ(b−a)Γ(b−2)))=(((b−1)(b−2)Γ(b−2)Γ(b−a−2))/((b−a−1)(b−a−2)Γ(b−a−2)Γ(b−2))) =(((b−1)(b−2))/((b−a−1)(b−a−2))) 2F_1 (a,1,b,1)=((Γ(b)Γ(b−a−1))/(Γ(b−a)Γ(b−1)))=(((b−1)Γ(b−1)Γ(b−a−1))/((b−a−1)Γ(b−a−1)Γ(b−1))) =((b−1)/(b−a−1)) S=2F_1 (a,2,b,1)−2F_1 (a,1,b,1)= S=(((b−1)(b−2))/((b−a−1)(b−a−2)))−((b−1)/((b−a−1)))=((b−1)/(b−a−1)).(((b−2)/(b−a−2))−1) =(((b−1))/((b−a−1)))((a/(b−a−2)))=((a(b−1))/((b−a−1)(b−a−2))) what i used 2F_1 (a,b,c,z)=Σ((a_n .b_n )/c_n ).(z^n /(n!)) (n+1)!=1.2......(n+2−1) n=1.2.....(n+1−1) β(x,y)=∫_0 ^1 t^(x−1) .(1−t)^(y−1) dt=((Γ(x).Γ(y))/(Γ(x+y)))
$$=\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}−\mathrm{1}\right)\mathrm{a}_{\mathrm{n}} }{\mathrm{b}_{\mathrm{n}} }=\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\mathrm{n}+\mathrm{1}\right)!.\mathrm{a}_{\mathrm{n}} }{\mathrm{b}_{\mathrm{n}} .\mathrm{n}!}−\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{n}!.\mathrm{a}_{\mathrm{n}} }{\mathrm{n}!.\mathrm{b}_{\mathrm{n}} }=\mathrm{S} \\ $$$$\mathrm{a}_{\mathrm{n}} =\mathrm{a}\left(\mathrm{a}+\mathrm{1}\right)…\left(\mathrm{a}+\mathrm{n}−\mathrm{1}\right) \\ $$$$\:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{z}\right)=\mathrm{1}+\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{a}_{\mathrm{n}} .\mathrm{b}_{\mathrm{n}} }{\mathrm{c}_{\mathrm{n}} }.\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$=\:\underset{\mathrm{z}\rightarrow\mathrm{1}} {\mathrm{lim}}\left\{\:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{2},\mathrm{b},\mathrm{z}\right)−_{\mathrm{2}} \:\mathrm{F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{1},\mathrm{b},\mathrm{z}\right)\right\} \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}\right).\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{z}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{b}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{c}−\mathrm{b}−\mathrm{1}} \left(\mathrm{1}−\mathrm{zx}\right)^{−\mathrm{a}} \mathrm{dx} \\ $$$$\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}\right)\:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{b}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{c}−\mathrm{b}−\mathrm{a}−\mathrm{1}} \mathrm{dx} \\ $$$$\Rightarrow\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}\right)\:\:_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{1}\right)=\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}−\mathrm{a}\right) \\ $$$$\Rightarrow_{\mathrm{2}} \mathrm{F}_{\mathrm{1}} =\frac{\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}−\mathrm{a}\right)}{\beta\left(\mathrm{b},\mathrm{c}−\mathrm{b}\right)}=\frac{\Gamma\left(\mathrm{b}\right)\Gamma\left(\mathrm{c}−\mathrm{b}−\mathrm{a}\right)\Gamma\left(\mathrm{c}\right)}{\Gamma\left(\mathrm{c}−\mathrm{a}\right)\Gamma\left(\mathrm{b}\right)\Gamma\left(\mathrm{c}−\mathrm{b}\right)}\Leftrightarrow \\ $$$$\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{1}\right)=\frac{\Gamma\left(\mathrm{c}\right).\Gamma\left(\mathrm{c}−\mathrm{a}−\mathrm{b}\right)}{\Gamma\left(\mathrm{c}−\mathrm{a}\right)\Gamma\left(\mathrm{c}−\mathrm{b}\right)} \\ $$$$\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{2},\mathrm{b},\mathrm{1}\right)=\frac{\Gamma\left(\mathrm{b}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)}{\Gamma\left(\mathrm{b}−\mathrm{a}\right)\Gamma\left(\mathrm{b}−\mathrm{2}\right)}=\frac{\left(\mathrm{b}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{2}\right)\Gamma\left(\mathrm{b}−\mathrm{2}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)\Gamma\left(\mathrm{b}−\mathrm{2}\right)} \\ $$$$=\frac{\left(\mathrm{b}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{2}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)} \\ $$$$\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{1},\mathrm{b},\mathrm{1}\right)=\frac{\Gamma\left(\mathrm{b}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)}{\Gamma\left(\mathrm{b}−\mathrm{a}\right)\Gamma\left(\mathrm{b}−\mathrm{1}\right)}=\frac{\left(\mathrm{b}−\mathrm{1}\right)\Gamma\left(\mathrm{b}−\mathrm{1}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\Gamma\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\Gamma\left(\mathrm{b}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{b}−\mathrm{1}}{\mathrm{b}−\mathrm{a}−\mathrm{1}} \\ $$$$\mathrm{S}=\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{2},\mathrm{b},\mathrm{1}\right)−\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{1},\mathrm{b},\mathrm{1}\right)= \\ $$$$\mathrm{S}=\frac{\left(\mathrm{b}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{2}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)}−\frac{\mathrm{b}−\mathrm{1}}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)}=\frac{\mathrm{b}−\mathrm{1}}{\mathrm{b}−\mathrm{a}−\mathrm{1}}.\left(\frac{\mathrm{b}−\mathrm{2}}{\mathrm{b}−\mathrm{a}−\mathrm{2}}−\mathrm{1}\right) \\ $$$$=\frac{\left(\mathrm{b}−\mathrm{1}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)}\left(\frac{\mathrm{a}}{\mathrm{b}−\mathrm{a}−\mathrm{2}}\right)=\frac{\mathrm{a}\left(\mathrm{b}−\mathrm{1}\right)}{\left(\mathrm{b}−\mathrm{a}−\mathrm{1}\right)\left(\mathrm{b}−\mathrm{a}−\mathrm{2}\right)} \\ $$$$\mathrm{what}\:\mathrm{i}\:\mathrm{used}\:\:\:\mathrm{2F}_{\mathrm{1}} \left(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{z}\right)=\Sigma\frac{\mathrm{a}_{\mathrm{n}} .\mathrm{b}_{\mathrm{n}} }{\mathrm{c}_{\mathrm{n}} }.\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)!=\mathrm{1}.\mathrm{2}……\left(\mathrm{n}+\mathrm{2}−\mathrm{1}\right) \\ $$$$\mathrm{n}=\mathrm{1}.\mathrm{2}…..\left(\mathrm{n}+\mathrm{1}−\mathrm{1}\right) \\ $$$$\beta\left(\mathrm{x},\mathrm{y}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}^{\mathrm{x}−\mathrm{1}} .\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{y}−\mathrm{1}} \mathrm{dt}=\frac{\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{y}\right)}{\Gamma\left(\mathrm{x}+\mathrm{y}\right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *