for-f-x-dx-F-x-c-and-sgn-x-x-x-x-x-x-0-let-sgn-x-0-for-x-0-does-sgn-f-x-f-x-dx-sgn-f-x-f-x-dx-sgn-f-x-is-just-a-constant-1-or-0-

Question Number 4344 by Filup last updated on 12/Jan/16

for \int f (x) d x = F (x) + c

and s g n (x) = \frac{x}{∣ x ∣} = \frac{∣ x ∣}{x} \forall x \neq 0

let sgn (x) = 0 for x = 0

does

\int s g n (f (x)) f (x) d x = s g n (f (x)) \int f (x) d x

∵ s g n (f (x)) is just a constant \pm 1 or 0 .

Commented by Filup last updated on 12/Jan/16

Let f (x) = x

sgn (x) x = x \frac{∣ x ∣}{x} = x \frac{x}{∣ x ∣} =∣ x ∣

N . B . : \frac{x^{2}}{∣ x ∣} =∣ x ∣ ∵ x^{2} \land ∣ x ∣> 0

S_{1} = \int sgn (x) x d x

= \int ∣ x ∣ d x (1)

S_{2} = sgn (x) \int x d x

= \frac{1}{2} sgn (x) x^{2} + c

= \frac{1}{2} ∣ x ∣ x + c (2)

if true :

\frac{d}{d x} (\frac{1}{2} ∣ x ∣ x + c) =∣ x ∣

\frac{d}{d x} (∣ x ∣) = \frac{d}{d x} ({(x^{2})}^{\frac{1}{2}})

= \frac{1}{2} {(x^{2})}^{- \frac{1}{2}} 2 x

= \frac{x}{∣ x ∣}

\frac{d}{d x} (\frac{1}{2} ∣ x ∣ x + c) = \frac{1}{2} (u^{'} v + {u v}^{'}) + 0

u =∣ x ∣ v = x

u^{'} = \frac{x}{∣ x ∣} v^{'} = 1

= \frac{1}{2} (\frac{x^{2}}{∣ x ∣} + ∣ x ∣)

= \frac{1}{2} (∣ x ∣ + ∣ x ∣)

=∣ x ∣

∴ \int sgn (x) x d x = sgn (x) \int x d x

Can we prove that the above is true / false

for limits - 1 ⩽ x ⩽ 1 ?

Commented by prakash jain last updated on 11/Jan/16

If f (x) is such that it does not change sign

within the limits of integration . You

can take out .

Commented by 123456 last updated on 11/Jan/16

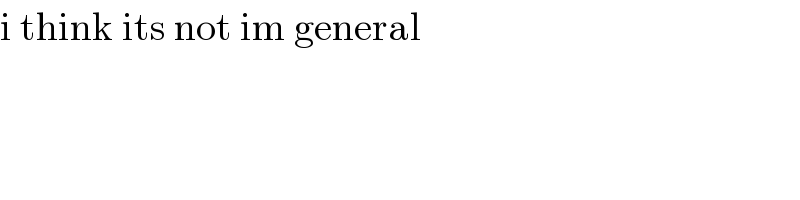
i think its not im general

Commented by Filup last updated on 12/Jan/16

\int_{- 1}^{1} f (x) d x = \int_{- 1}^{0} f (x) d x + \int_{0}^{1} f (x) d x

∴ if true :

\int_{- 1}^{0} sgn (x) x d x + \int_{0}^{1} sgn (x) x d x = sgn (x) \int_{- 1}^{0} x d x + sgn (x) \int_{0}^{1} x d x

\overset{? ? ?}{\Rightarrow} \int_{- 1}^{0} sgn (x) x d x + \int_{0}^{1} sgn (x) x d x = sgn (x) (\int_{- 1}^{0} x d x + \int_{0}^{1} x d x)

Facebook Tweet Pin