Question Number 2231 by Filup last updated on 10/Nov/15

$$\mathrm{For}\:{f}\left({x}\right)={x}! \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{defined}: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{f}'\left({x}\right) \\ $$$$\left(\mathrm{2}\right)\:\int{f}\left({x}\right){dx} \\ $$
Commented by Filup last updated on 10/Nov/15
![Is this a correct assumption for (1): y=x! y=x(x−1)(x−2)... ∴y=Π_(i=1) ^x i Using Chain rule: ∴y′=[(x−1)(x−2)...]+[x(x−2)...]+... y′=(y/x)+(y/(x−1))+...=y((1/x)+(1/(x−1))+...+1) y′=yΣ_(i=1) ^(x−1) ((1/i)) ∴y′=y∙H(x−1) where H(n) is the sum to the nth harmonic term y=Π_(i=1) ^x i y′=yΣ_(i=1) ^(x−1) (1/i) Note: I have no knowledge of differentiating this function, so this is only a guess attempt](https://www.tinkutara.com/question/Q2232.png)
$$\mathrm{Is}\:\mathrm{this}\:\mathrm{a}\:\mathrm{correct}\:\mathrm{assumption}\:\mathrm{for}\:\left(\mathrm{1}\right): \\ $$$$ \\ $$$${y}={x}! \\ $$$${y}={x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)… \\ $$$$\therefore{y}=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i} \\ $$$$ \\ $$$${Using}\:{Chain}\:{rule}: \\ $$$$\therefore{y}'=\left[\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)…\right]+\left[{x}\left({x}−\mathrm{2}\right)…\right]+… \\ $$$${y}'=\frac{{y}}{{x}}+\frac{{y}}{{x}−\mathrm{1}}+…={y}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}−\mathrm{1}}+…+\mathrm{1}\right) \\ $$$${y}'={y}\underset{{i}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\sum}}\left(\frac{\mathrm{1}}{{i}}\right) \\ $$$$\therefore{y}'={y}\centerdot\mathrm{H}\left({x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{where}\:\mathrm{H}\left({n}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{to}\:\mathrm{the}\:{n}\mathrm{th} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{harmonic}\:\mathrm{term} \\ $$$${y}=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i} \\ $$$${y}'={y}\underset{{i}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$$ \\ $$$$\mathrm{Note}:\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{knowledge}\:\mathrm{of}\:\mathrm{differentiating} \\ $$$$\mathrm{this}\:\mathrm{function},\:\mathrm{so}\:\mathrm{this}\:\mathrm{is}\:\mathrm{only}\:\mathrm{a}\:\mathrm{guess}\:\mathrm{attempt} \\ $$
Commented by 123456 last updated on 10/Nov/15
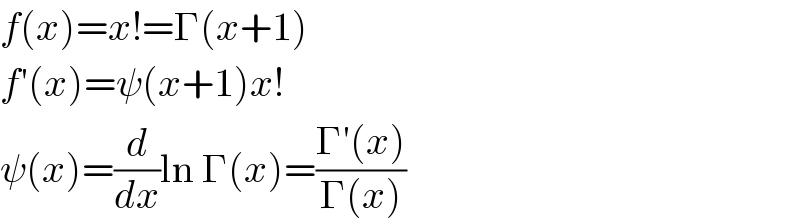
$${f}\left({x}\right)={x}!=\Gamma\left({x}+\mathrm{1}\right) \\ $$$${f}'\left({x}\right)=\psi\left({x}+\mathrm{1}\right){x}! \\ $$$$\psi\left({x}\right)=\frac{{d}}{{dx}}\mathrm{ln}\:\Gamma\left({x}\right)=\frac{\Gamma'\left({x}\right)}{\Gamma\left({x}\right)} \\ $$
