Question Number 131622 by rydasss last updated on 06/Feb/21
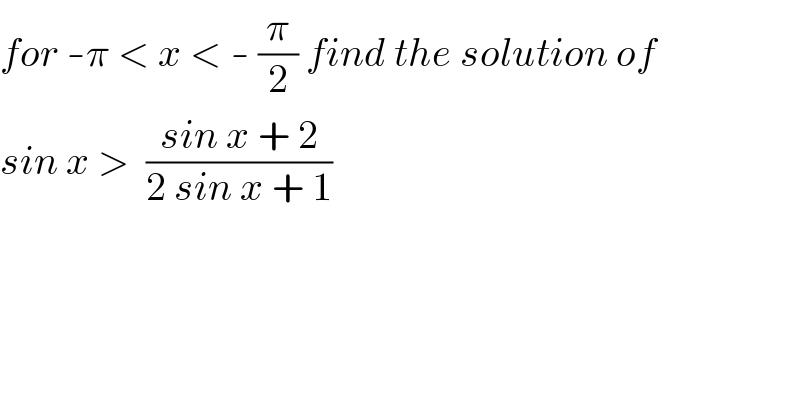
$${for}\:-\pi\:<\:{x}\:<\:-\:\frac{\pi}{\mathrm{2}}\:{find}\:{the}\:{solution}\:{of} \\ $$$${sin}\:{x}\:>\:\:\frac{{sin}\:{x}\:+\:\mathrm{2}}{\mathrm{2}\:{sin}\:{x}\:+\:\mathrm{1}} \\ $$
Answered by mr W last updated on 07/Feb/21
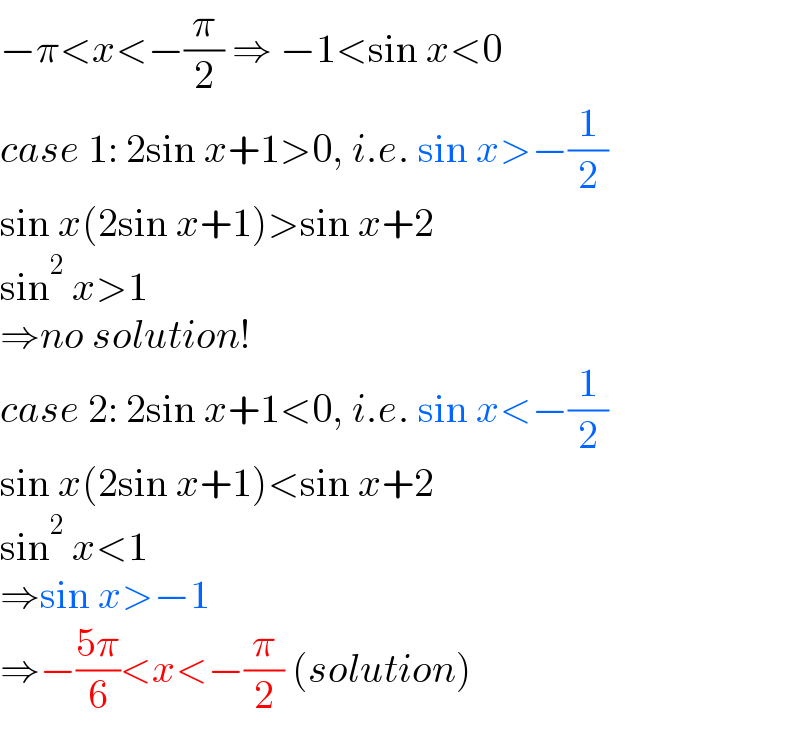
$$−\pi<{x}<−\frac{\pi}{\mathrm{2}}\:\Rightarrow\:−\mathrm{1}<\mathrm{sin}\:{x}<\mathrm{0} \\ $$$${case}\:\mathrm{1}:\:\mathrm{2sin}\:{x}+\mathrm{1}>\mathrm{0},\:{i}.{e}.\:\mathrm{sin}\:{x}>−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{2sin}\:{x}+\mathrm{1}\right)>\mathrm{sin}\:{x}+\mathrm{2} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}>\mathrm{1} \\ $$$$\Rightarrow{no}\:{solution}! \\ $$$${case}\:\mathrm{2}:\:\mathrm{2sin}\:{x}+\mathrm{1}<\mathrm{0},\:{i}.{e}.\:\mathrm{sin}\:{x}<−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{2sin}\:{x}+\mathrm{1}\right)<\mathrm{sin}\:{x}+\mathrm{2} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}<\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:{x}>−\mathrm{1} \\ $$$$\Rightarrow−\frac{\mathrm{5}\pi}{\mathrm{6}}<{x}<−\frac{\pi}{\mathrm{2}}\:\left({solution}\right) \\ $$
Commented by rydasss last updated on 07/Feb/21
$${Thank}\:{you}\:{so}\:{much}. \\ $$
