for-the-extremum-values-of-x-2-y-2-z-2-subject-to-the-constraints-ax-2-by-2-cz-2-1-and-lx-my-nz-0-show-that-the-stationary-points-setisfy-the-realation-l-2-1-a-1-m-2-1-b-1-n-2-

Tinku Tara June 3, 2023 None 0 Comments

Question Number 133010 by rs4089 last updated on 18/Feb/21

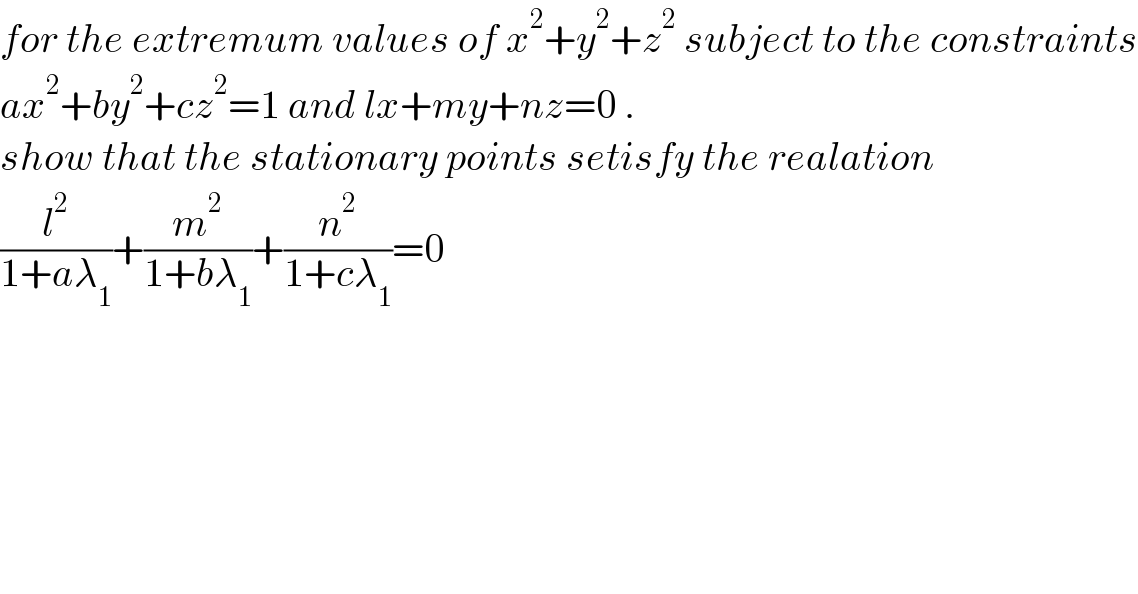
for the extremum values of x^2 +y^2 +z^2 subject to the constraints ax^2 +by^2 +cz^2 =1 and lx+my+nz=0 . show that the stationary points setisfy the realation (l^2 /(1+aλ_1 ))+(m^2 /(1+bλ_1 ))+(n^2 /(1+cλ_1 ))=0

$${for}\:{the}\:{extremum}\:{values}\:{of}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:{subject}\:{to}\:{the}\:{constraints} \\ $$$${ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +{cz}^{\mathrm{2}} =\mathrm{1}\:{and}\:{lx}+{my}+{nz}=\mathrm{0}\:. \\ $$$${show}\:{that}\:{the}\:{stationary}\:{points}\:{setisfy}\:{the}\:{realation} \\ $$$$\frac{{l}^{\mathrm{2}} }{\mathrm{1}+{a}\lambda_{\mathrm{1}} }+\frac{{m}^{\mathrm{2}} }{\mathrm{1}+{b}\lambda_{\mathrm{1}} }+\frac{{n}^{\mathrm{2}} }{\mathrm{1}+{c}\lambda_{\mathrm{1}} }=\mathrm{0} \\ $$

Facebook Tweet Pin

for-the-extremum-values-of-x-2-y-2-z-2-subject-to-the-constraints-ax-2-by-2-cz-2-1-and-lx-my-nz-0-show-that-the-stationary-points-setisfy-the-realation-l-2-1-a-1-m-2-1-b-1-n-2-

Leave a Reply Cancel reply