Menu Close

For-vectors-v-and-u-where-v-u-R-n-What-is-the-angle-between-v-and-u-both-are-from-origin-

Tinku Tara 0 Comments
Pin




Question Number 6875 by FilupSmith last updated on 01/Aug/16
For vectors v and u where: v,u∈R^n What is the angle between v and u? (both are from origin)
$$\mathrm{For}\:\mathrm{vectors}\:\boldsymbol{{v}}\:\mathrm{and}\:\boldsymbol{{u}}\:\mathrm{where}: \\ $$$$\boldsymbol{{v}},\boldsymbol{{u}}\in\mathbb{R}^{{n}} \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\boldsymbol{{v}}\:\mathrm{and}\:\boldsymbol{{u}}? \\ $$$$\left(\mathrm{both}\:\mathrm{are}\:\mathrm{from}\:\mathrm{origin}\right) \\ $$
Commented by prakash jain last updated on 01/Aug/16
cos θ=((v∙u)/(vu))
$$\mathrm{cos}\:\theta=\frac{\boldsymbol{{v}}\centerdot\boldsymbol{{u}}}{{vu}} \\ $$
Commented by FilupSmith last updated on 01/Aug/16
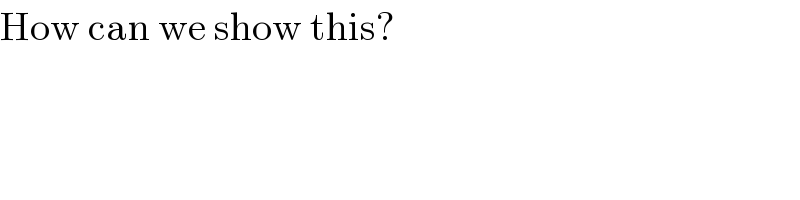
How can we show this?
$$\mathrm{How}\:\mathrm{can}\:\mathrm{we}\:\mathrm{show}\:\mathrm{this}? \\ $$
Commented by FilupSmith last updated on 01/Aug/16
Is this correct? c^2 =a^2 +b^2 −2abcosθ cosθ=((c^2 −a^2 −b^2 )/(−2ab)) c=Distance between v and u c=∥v−u∥=(√(∥v∥^2 +∥u∥^2 −2v∙u)) proof for this needed a=∥v∥=(√(v_1 ^2 +...+v_n ^2 ))=(√(Σ_(t=1) ^n v_t ^2 )) b=∥u∥=(√(u_1 ^2 +...+u_n ^2 ))=(√(Σ_(t=1) ^n u_t ^2 )) cosθ=−((∥v−u∥^2 −∥v∥^2 −∥u∥^2 )/(2∥v∥∥u∥)) cosθ=−((((√(∥v∥^2 +∥u∥^2 −2v∙u)))^2 −∥v∥^2 −∥u∥^2 )/(2∥v∥∥u∥)) cosθ=−((∥v∥^2 +∥u∥^2 −2v∙u−∥v∥^2 −∥u∥^2 )/(2∥v∥∥u∥)) cosθ=−((−2v∙u)/(2∥v∥∥u∥)) cosθ=((2v∙u)/(∥v∥∥u∥))=((2Σ_(t=1) ^n v_t u_t )/( (√((Σ_(t=1) ^n v_t ^2 )(Σ_(t=1) ^n u_t ^2 )))))
$$\mathrm{Is}\:\mathrm{this}\:\mathrm{correct}? \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\theta \\ $$$$\mathrm{cos}\theta=\frac{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{−\mathrm{2}{ab}} \\ $$$${c}=\mathrm{Distance}\:\mathrm{between}\:\boldsymbol{{v}}\:\mathrm{and}\:\boldsymbol{{u}} \\ $$$${c}=\parallel\boldsymbol{{v}}−\boldsymbol{{u}}\parallel=\sqrt{\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} +\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} −\mathrm{2}\boldsymbol{{v}}\centerdot\boldsymbol{{u}}}\:\:{proof}\:{for}\:{this}\:{needed} \\ $$$${a}=\parallel\boldsymbol{{v}}\parallel=\sqrt{{v}_{\mathrm{1}} ^{\mathrm{2}} +…+{v}_{{n}} ^{\mathrm{2}} }=\sqrt{\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}{v}_{{t}} ^{\mathrm{2}} } \\ $$$${b}=\parallel\boldsymbol{{u}}\parallel=\sqrt{{u}_{\mathrm{1}} ^{\mathrm{2}} +…+{u}_{{n}} ^{\mathrm{2}} }=\sqrt{\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{t}} ^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{cos}\theta=−\frac{\parallel\boldsymbol{{v}}−\boldsymbol{{u}}\parallel^{\mathrm{2}} −\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} −\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} }{\mathrm{2}\parallel\boldsymbol{{v}}\parallel\parallel\boldsymbol{{u}}\parallel} \\ $$$$\mathrm{cos}\theta=−\frac{\left(\sqrt{\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} +\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} −\mathrm{2}\boldsymbol{{v}}\centerdot\boldsymbol{{u}}}\right)^{\mathrm{2}} −\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} −\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} }{\mathrm{2}\parallel\boldsymbol{{v}}\parallel\parallel\boldsymbol{{u}}\parallel} \\ $$$$\mathrm{cos}\theta=−\frac{\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} +\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} −\mathrm{2}\boldsymbol{{v}}\centerdot\boldsymbol{{u}}−\parallel\boldsymbol{{v}}\parallel^{\mathrm{2}} −\parallel\boldsymbol{{u}}\parallel^{\mathrm{2}} }{\mathrm{2}\parallel\boldsymbol{{v}}\parallel\parallel\boldsymbol{{u}}\parallel} \\ $$$$\mathrm{cos}\theta=−\frac{−\mathrm{2}\boldsymbol{{v}}\centerdot\boldsymbol{{u}}}{\mathrm{2}\parallel\boldsymbol{{v}}\parallel\parallel\boldsymbol{{u}}\parallel} \\ $$$$\mathrm{cos}\theta=\frac{\mathrm{2}\boldsymbol{{v}}\centerdot\boldsymbol{{u}}}{\parallel\boldsymbol{{v}}\parallel\parallel\boldsymbol{{u}}\parallel}=\frac{\mathrm{2}\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}{v}_{{t}} {u}_{{t}} }{\:\sqrt{\left(\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}{v}_{{t}} ^{\mathrm{2}} \right)\left(\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{t}} ^{\mathrm{2}} \right)}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *