Question Number 2341 by Rasheed Soomro last updated on 17/Nov/15
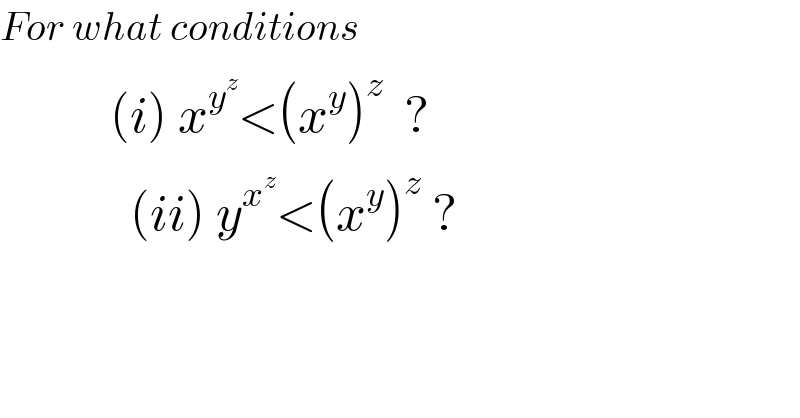
$${For}\:{what}\:{conditions} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left({i}\right)\:{x}^{{y}^{{z}} } <\left({x}^{{y}} \right)^{{z}} \:\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:{y}^{{x}^{{z}} } <\left({x}^{{y}} \right)^{{z}} \:? \\ $$
Commented by prakash jain last updated on 19/Nov/15

$$\left({i}\right)\:{x}^{{y}^{{z}} } <\left({x}^{{y}} \right)^{{z}} \\ $$$$\mathrm{A}.\:{z}=\mathrm{1}\vee{x}=\mathrm{1}\vee{y}=\mathrm{1}\vee{x}=\mathrm{0}\vee{y}=\mathrm{0}\vee{z}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{not}\:\mathrm{satisfied} \\ $$$$\mathrm{B}.\:{z}>\mathrm{1} \\ $$$$\mathrm{B1}.\:\mathrm{case}\:{x}>\mathrm{1},{y}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{y}^{{z}} \mathrm{ln}\:{x}<{yz}\mathrm{ln}\:{x}\Rightarrow{y}^{{z}} <{yz}\:\because\left({x}>\mathrm{1},\:\mathrm{ln}\:{x}>\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\left({z}−\mathrm{1}\right)\mathrm{ln}\:{y}<\mathrm{ln}\:{z} \\ $$$$\:\:\:\:\:\:\:\:\:{y}<{z}^{\mathrm{1}/\left({z}−\mathrm{1}\right)} \\ $$$$\mathrm{B2}.\:\mathrm{0}<{x}<\mathrm{1},\:{y}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{y}^{{z}} \mathrm{ln}\:{x}<{yz}\mathrm{ln}\:{x}\Rightarrow{y}^{{z}} >{yz}\:\because\left({x}>\mathrm{1},\:\mathrm{ln}\:{x}>\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:{y}>{z}^{\mathrm{1}/\left({z}−\mathrm{1}\right)} \\ $$$$\mathrm{More}\:\mathrm{cases}\:\mathrm{can}\:\mathrm{be}\:\mathrm{considered}\:\mathrm{similarly}. \\ $$$${only}\:{integers}\:{need}\:{to}\:{be}\:{considered}\:{for} \\ $$$$−{ve}\:{numbers}.\:{otherwise}\:{result}\:{will}\:{be}\:{complex}. \\ $$
Commented by Rasheed Soomro last updated on 18/Nov/15

$$\overset{\mathcal{VERY}} {\mathcal{NICE}}\:! \\ $$
