For-x-y-n-n-Z-x-y-n-u-0-n-n-u-x-n-u-y-n-Is-there-a-generalization-for-when-n-is-non-integer-e-g-x-y-1-n-n-1-Z-

Question Number 9784 by FilupSmith last updated on 04/Jan/17

For {(x + y)}^{n} : n \in Z

{(x + y)}^{n} = \underset{u = 0}{\sum^{n}} (\begin{matrix} n \\ u \end{matrix}) x^{n - u} y^{n}

Is there a generalization for when

n is non integer ?

e . g . {(x + y)}^{1 / n} : n^{- 1} \notin Z

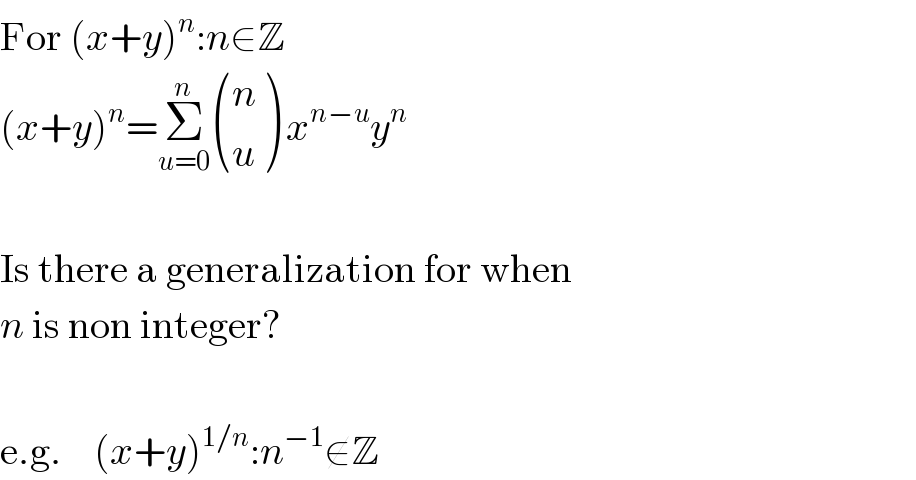
Commented by FilupSmith last updated on 05/Jan/17

Taylor Series :

f (x) = {(x + y)}^{N} N \in C

f (x) = \underset{u = 0}{\sum^{\infty}} \frac{f^{(u)} (a)}{u!} {(x - a)}^{u}

a = 1 - y

f (x) = \underset{u = 0}{\sum^{\infty}} \frac{f^{(u)} (1 - y)}{u!} {(x + y - 1)}^{u}

f (x) = \frac{{(1 - y + y)}^{N}}{0!} {(x + y + 1)}^{0} + \frac{N {(1 - y + y)}^{N - 1}}{1!} {(x + y - 1)}^{1} + \dots

∴ f (x) = 1 + N (x + y - 1) + \frac{1}{2} N (N - 1) {(x + y - 1)}^{2} + \frac{1}{4} N (N - 1) (N - 2) {(x + y - 1)}^{3} + \dots

f (x) = {(x + y)}^{N} = \underset{u = 0}{\sum^{\infty}} (\frac{N! \cdot {(x + y - 1)}^{u}}{u! \cdot (N - u)!})

N \notin Z

= \underset{u = 0}{\sum^{\infty}} (\frac{Γ (N + 1) \cdot {(x + y - 1)}^{u}}{u! \cdot Γ (N + 1 - u)})

∴ f (x) = {(x + y)}^{N} = \underset{u = 0}{\sum^{\infty}} (\frac{Γ (N + 1)}{u! \cdot Γ (N + 1 - u)} {(x + y - 1)}^{u})

if N \in Z

= \underset{u = 0}{\sum^{\infty}} ((\begin{matrix} N \\ u \end{matrix}) {(x + y - 1)}^{u})

Commented by prakash jain last updated on 04/Jan/17

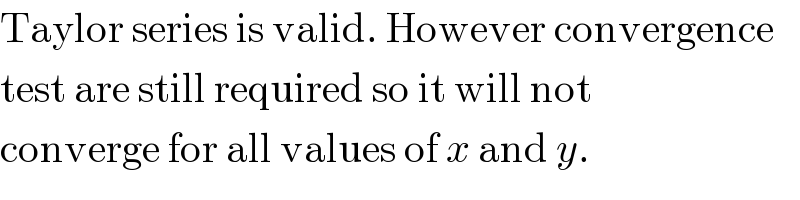
Taylor series is valid . However convergence

test are still required so it will not

converge for all values of x and y .

Commented by FilupSmith last updated on 05/Jan/17

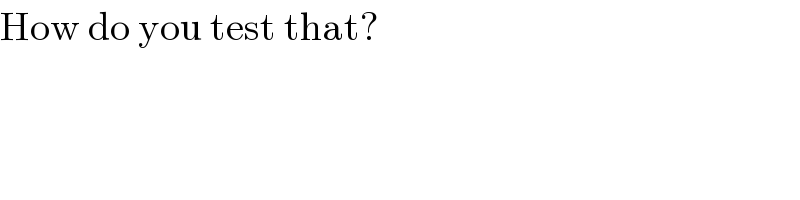
How do you test that ?

Commented by FilupSmith last updated on 05/Jan/17

f (x) = \underset{u = 0}{\sum^{\infty}} (\frac{Γ (N + 1)}{u! \cdot Γ (N + 1 - u)} {(x + y - 1)}^{u})

Converges if L = \lim_{n \to \infty} ∣ \frac{a_{n + 1}}{a_{n}} ∣< 1

L = \lim_{u \to \infty} ∣ \frac{\frac{Γ (N + 1)}{(u + 1)! \cdot Γ (N + 1 - u - 1)} {(x + y - 1)}^{u + 1}}{\frac{Γ (N + 1)}{u! \cdot Γ (N + 1 - u)} {(x + y - 1)}^{u}} ∣

L = \lim_{u \to \infty} ∣ \frac{Γ (N + 1) {(x + y - 1)}^{u + 1}}{(u + 1)! \cdot Γ (N + 1 - u - 1)} \times \frac{u! \cdot Γ (N + 1 - u)}{Γ (N + 1) {(x + y - 1)}^{u}} ∣

L = \lim_{u \to \infty} ∣ \frac{(x + y - 1)}{(u + 1)! \cdot Γ (N + 1 - u - 1)} \times \frac{u! \cdot Γ (N + 1 - u)}{1} ∣

L = \lim_{u \to \infty} ∣ \frac{(x + y - 1)}{(u + 1) \cdot Γ (N - u)} \times \frac{Γ (N - u + 1)}{1} ∣

L = \lim_{u \to \infty} ∣ \frac{(x + y - 1) \cdot (N - u + 1)}{(u + 1)} \times \frac{1}{1} ∣

L = \lim_{u \to \infty} ∣ \frac{(x + y - 1) (N - u + 1)}{(u + 1)} ∣

L^{'} {H o p i t a l}^{'} s L a w

L = \lim_{u \to \infty} ∣ \frac{(x + y - 1) (- 1)}{1} ∣

L =∣ - (x + y - 1) ∣

If L < 1, f (x) converges

∴∣ x + y - 1 ∣< 1

f (x) = {(x + y)}^{N} = \underset{u = 0}{\sum^{\infty}} (\frac{Γ (N + 1)}{u! \cdot Γ (N + 1 - u)} {(x + y - 1)}^{u})

if : ∣ x + y - 1 ∣< 1