Question Number 2163 by Filup last updated on 06/Nov/15

$$\mathrm{For}:\:{y}={f}\left({x}\right)\:\rightarrow\:{x}={g}\left({y}\right) \\ $$$$\mathrm{Therefore}: \\ $$$$\begin{cases}{{x}\left({t}\right)={t}}\\{{y}\left({t}\right)={f}\left({t}\right)}\end{cases} \\ $$$$\mathrm{let}\:\boldsymbol{{r}}\left({t}\right)=\langle{x}\left({t}\right),\:{y}\left({t}\right)\rangle \\ $$$$ \\ $$$$\therefore\int\boldsymbol{{r}}{dt}=\langle\int{tdt},\:\int{f}\left({t}\right){dt}\rangle \\ $$$$ \\ $$$$\mathrm{Does}: \\ $$$$\int{x}\left({t}\right){dt}=\int{g}\left({y}\right){dy} \\ $$$$\mathrm{and} \\ $$$$\int{y}\left({t}\right){dt}=\int{f}\left({x}\right){dx} \\ $$
Commented by prakash jain last updated on 06/Nov/15
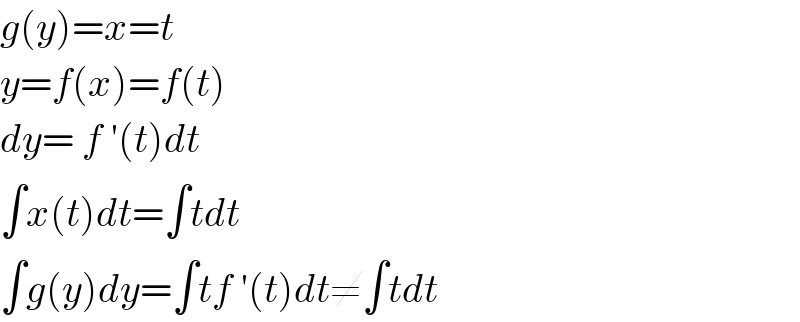
$${g}\left({y}\right)={x}={t} \\ $$$${y}={f}\left({x}\right)={f}\left({t}\right) \\ $$$${dy}=\:{f}\:'\left({t}\right){dt} \\ $$$$\int{x}\left({t}\right){dt}=\int{tdt} \\ $$$$\int{g}\left({y}\right){dy}=\int{tf}\:'\left({t}\right){dt}\neq\int{tdt} \\ $$
Answered by prakash jain last updated on 06/Nov/15
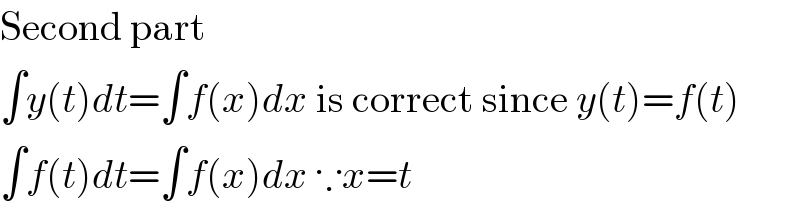
$$\mathrm{Second}\:\mathrm{part}\: \\ $$$$\int{y}\left({t}\right){dt}=\int{f}\left({x}\right){dx}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{since}\:{y}\left({t}\right)={f}\left({t}\right) \\ $$$$\int{f}\left({t}\right){dt}=\int{f}\left({x}\right){dx}\:\because{x}={t} \\ $$
Commented by Filup last updated on 06/Nov/15

$$\mathcal{T}{hanks} \\ $$
