Menu Close

For-y-x-2-show-how-to-find-dy-d-

Tinku Tara 0 Comments
Pin




Question Number 9498 by FilupSmith last updated on 11/Dec/16
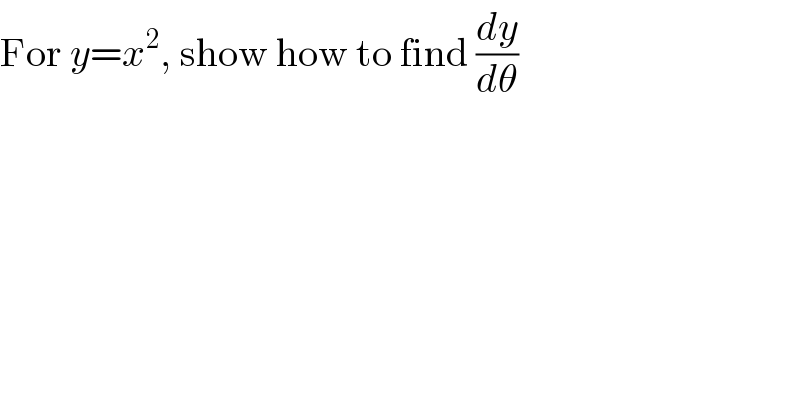
For y=x^2 , show how to find (dy/dθ)
$$\mathrm{For}\:{y}={x}^{\mathrm{2}} ,\:\mathrm{show}\:\mathrm{how}\:\mathrm{to}\:\mathrm{find}\:\frac{{dy}}{{d}\theta} \\ $$
Commented by FilupSmith last updated on 11/Dec/16
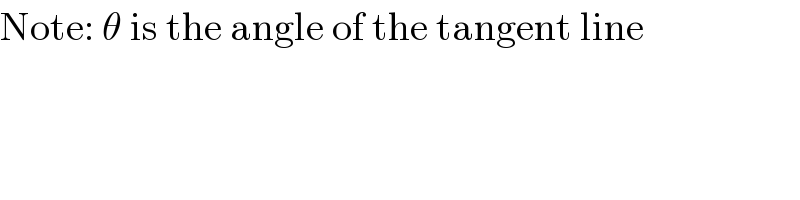
Note: θ is the angle of the tangent line
$$\mathrm{Note}:\:\theta\:\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{line} \\ $$
Answered by mrW last updated on 11/Dec/16
tan θ=(dy/dx)=2x θ=tan^(−1) (2x) Way I: y=x^2 =((1/2)tan θ)^2 =(1/4)tan^2 θ (dy/dθ)=(1/4)×2tan θ×(1/(cos^2 θ))=(1/2)×tan θ×(1+tan^2 θ)=x(1+4x^2 ) Way II: (dθ/dx)=(1/(1+(2x)^2 ))×2=(2/(1+4x^2 )) (dy/dθ)=(dy/dx)×(dx/dθ)=(dy/dx)×(1/(dθ/dx))=(2x)(1/(2/(1+4x^2 )))=x(1+4x^2 ) Since both y and θ are already expressed in terms of x, in most cases way II is easier than way I.
$$\mathrm{tan}\:\theta=\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{2x} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2x}\right) \\ $$$$ \\ $$$$\mathrm{Way}\:\mathrm{I}: \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:\theta\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \theta \\ $$$$\frac{\mathrm{dy}}{\mathrm{d}\theta}=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2tan}\:\theta×\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \theta}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{tan}\:\theta×\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta\right)=\mathrm{x}\left(\mathrm{1}+\mathrm{4x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$$\mathrm{Way}\:\mathrm{II}: \\ $$$$\frac{\mathrm{d}\theta}{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{2x}\right)^{\mathrm{2}} }×\mathrm{2}=\frac{\mathrm{2}}{\mathrm{1}+\mathrm{4x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{dy}}{\mathrm{d}\theta}=\frac{\mathrm{dy}}{\mathrm{dx}}×\frac{\mathrm{dx}}{\mathrm{d}\theta}=\frac{\mathrm{dy}}{\mathrm{dx}}×\frac{\mathrm{1}}{\frac{\mathrm{d}\theta}{\mathrm{dx}}}=\left(\mathrm{2x}\right)\frac{\mathrm{1}}{\frac{\mathrm{2}}{\mathrm{1}+\mathrm{4x}^{\mathrm{2}} }}=\mathrm{x}\left(\mathrm{1}+\mathrm{4x}^{\mathrm{2}} \right) \\ $$$$ \\ $$$${Since}\:{both}\:{y}\:{and}\:\theta\:{are}\:{already}\: \\ $$$${expressed}\:{in}\:{terms}\:{of}\:{x},\:{in}\:{most} \\ $$$${cases}\:{way}\:{II}\:{is}\:{easier}\:{than}\:{way}\:{I}. \\ $$
Commented by FilupSmith last updated on 11/Dec/16
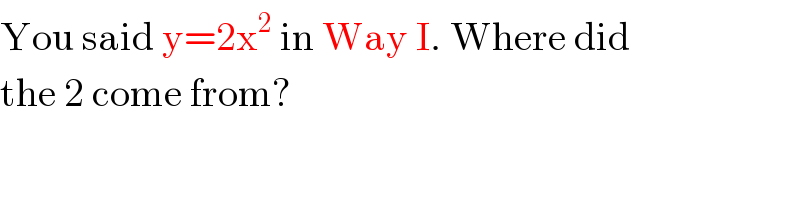
You said y=2x^2 in Way I. Where did the 2 come from?
$$\mathrm{You}\:\mathrm{said}\:\mathrm{y}=\mathrm{2x}^{\mathrm{2}} \:\mathrm{in}\:\mathrm{Way}\:\mathrm{I}.\:\mathrm{Where}\:\mathrm{did} \\ $$$$\mathrm{the}\:\mathrm{2}\:\mathrm{come}\:\mathrm{from}? \\ $$
Commented by mrW last updated on 11/Dec/16
sorry, that′s my mistake, I′ll correct.
$$\mathrm{sorry},\:\mathrm{that}'\mathrm{s}\:\mathrm{my}\:\mathrm{mistake},\:\mathrm{I}'\mathrm{ll}\:\mathrm{correct}. \\ $$
Commented by mrW last updated on 11/Dec/16
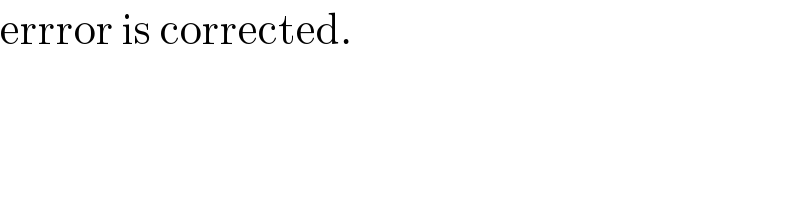
errror is corrected.
$$\mathrm{errror}\:\mathrm{is}\:\mathrm{corrected}. \\ $$
Commented by FilupSmith last updated on 11/Dec/16
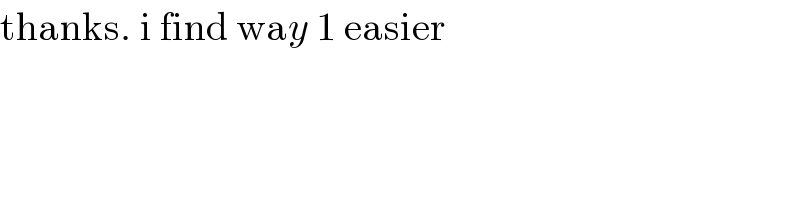
thanks. i find way 1 easier
$$\mathrm{thanks}.\:\mathrm{i}\:\mathrm{find}\:\mathrm{wa}{y}\:\mathrm{1}\:\mathrm{easier} \\ $$
Commented by mrW last updated on 11/Dec/16
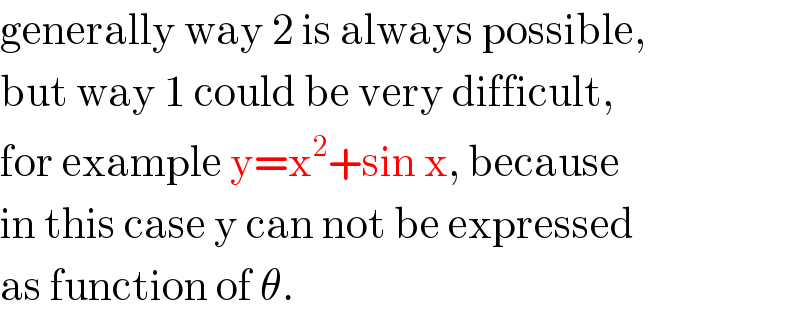
generally way 2 is always possible, but way 1 could be very difficult, for example y=x^2 +sin x, because in this case y can not be expressed as function of θ.
$$\mathrm{generally}\:\mathrm{way}\:\mathrm{2}\:\mathrm{is}\:\mathrm{always}\:\mathrm{possible}, \\ $$$$\mathrm{but}\:\mathrm{way}\:\mathrm{1}\:\mathrm{could}\:\mathrm{be}\:\mathrm{very}\:\mathrm{difficult}, \\ $$$$\mathrm{for}\:\mathrm{example}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} +\mathrm{sin}\:\mathrm{x},\:\mathrm{because} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{y}\:\mathrm{can}\:\mathrm{not}\:\mathrm{be}\:\mathrm{expressed} \\ $$$$\mathrm{as}\:\mathrm{function}\:\mathrm{of}\:\theta. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *