Question Number 133191 by pticantor last updated on 19/Feb/21
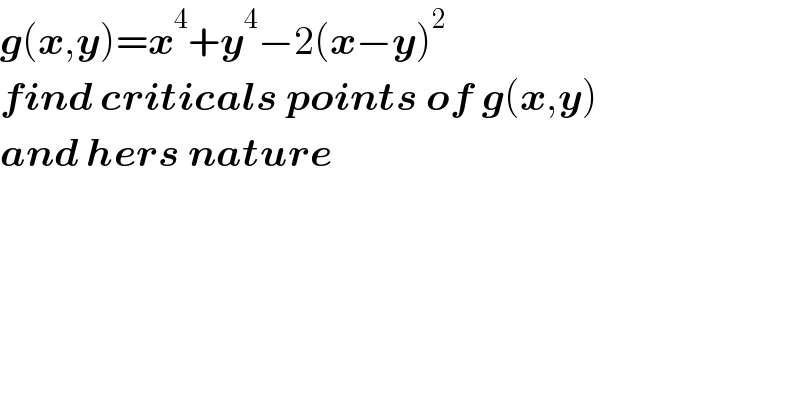
$$\boldsymbol{{g}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)=\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{y}}^{\mathrm{4}} −\mathrm{2}\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{{find}}\:\boldsymbol{{criticals}}\:\boldsymbol{{points}}\:\boldsymbol{{of}}\:\boldsymbol{{g}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right) \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{hers}}\:\boldsymbol{{nature}} \\ $$
Answered by Olaf last updated on 20/Feb/21
![g(x,y) = x^4 +y^4 −2(x−y)^2 ▽g = [((∂g/∂x)),((∂g/∂y)) ] = [((4x^3 −2(x−y))),((4y^3 +2(x−y))) ] ▽g = [(0),(0) ]⇔ (x−y) = 2x^3 = −2y^3 ⇔ (x,y) = (0,0) : this is the only critical point. Hessian matrix : [((∂^2 g/∂x^2 ),(∂^2 g/(∂x∂y))),((∂^2 g/(∂y∂x)),(∂^2 g/∂y^2 )) ] = [((12x^2 −2x),2),(2,(12y^2 −2y)) ] Hessian matrix in (0,0) : Hess(g)∣_((0,0)) = [(0,2),(2,0) ] det(Hess(g)∣_((0,0)) ) = determinant ((0,2),(2,0))= −4 det(Hess(g)∣_((0,0)) ) < 0 ⇒ (0,0) is a saddle point](https://www.tinkutara.com/question/Q133207.png)
$${g}\left({x},{y}\right)\:=\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} −\mathrm{2}\left({x}−{y}\right)^{\mathrm{2}} \\ $$$$\bigtriangledown{g}\:=\:\begin{bmatrix}{\frac{\partial{g}}{\partial{x}}}\\{\frac{\partial{g}}{\partial{y}}}\end{bmatrix}\:=\:\begin{bmatrix}{\mathrm{4}{x}^{\mathrm{3}} −\mathrm{2}\left({x}−{y}\right)}\\{\mathrm{4}{y}^{\mathrm{3}} +\mathrm{2}\left({x}−{y}\right)}\end{bmatrix} \\ $$$$\bigtriangledown{g}\:=\:\begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{bmatrix}\Leftrightarrow\:\left({x}−{y}\right)\:=\:\mathrm{2}{x}^{\mathrm{3}} \:=\:−\mathrm{2}{y}^{\mathrm{3}} \\ $$$$\Leftrightarrow\:\left({x},{y}\right)\:=\:\left(\mathrm{0},\mathrm{0}\right)\::\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only} \\ $$$$\mathrm{critical}\:\mathrm{point}. \\ $$$$ \\ $$$$\mathrm{Hessian}\:\mathrm{matrix}\:: \\ $$$$\begin{bmatrix}{\frac{\partial^{\mathrm{2}} {g}}{\partial{x}^{\mathrm{2}} }}&{\frac{\partial^{\mathrm{2}} {g}}{\partial{x}\partial{y}}}\\{\frac{\partial^{\mathrm{2}} {g}}{\partial{y}\partial{x}}}&{\frac{\partial^{\mathrm{2}} {g}}{\partial{y}^{\mathrm{2}} }}\end{bmatrix}\:=\:\begin{bmatrix}{\mathrm{12}{x}^{\mathrm{2}} −\mathrm{2}{x}}&{\mathrm{2}}\\{\mathrm{2}}&{\mathrm{12}{y}^{\mathrm{2}} −\mathrm{2}{y}}\end{bmatrix} \\ $$$$\mathrm{Hessian}\:\mathrm{matrix}\:\mathrm{in}\:\left(\mathrm{0},\mathrm{0}\right)\:: \\ $$$$\mathrm{Hess}\left({g}\right)\mid_{\left(\mathrm{0},\mathrm{0}\right)} \:=\:\begin{bmatrix}{\mathrm{0}}&{\mathrm{2}}\\{\mathrm{2}}&{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{det}\left(\mathrm{Hess}\left({g}\right)\mid_{\left(\mathrm{0},\mathrm{0}\right)} \right)\:=\:\begin{vmatrix}{\mathrm{0}}&{\mathrm{2}}\\{\mathrm{2}}&{\mathrm{0}}\end{vmatrix}=\:−\mathrm{4} \\ $$$$\mathrm{det}\left(\mathrm{Hess}\left({g}\right)\mid_{\left(\mathrm{0},\mathrm{0}\right)} \right)\:<\:\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{0},\mathrm{0}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{saddle}\:\mathrm{point} \\ $$
