Question Number 135570 by bemath last updated on 14/Mar/21
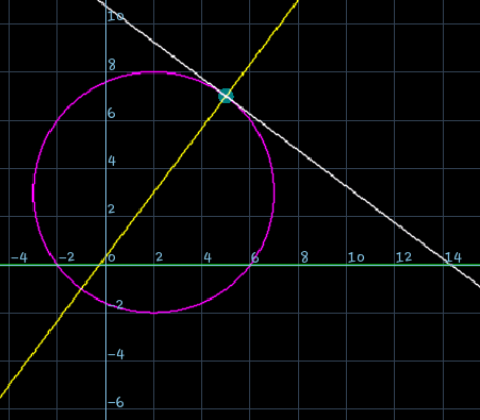
$${Geometry} \\ $$If the area of the triangle formed by the positive x-axis, the normal and the tangent to the circle (x-2) ² +(y-3) ² =25 at the point (5,7) is A, then 24A is equal to______?
Answered by EDWIN88 last updated on 14/Mar/21
Commented by EDWIN88 last updated on 14/Mar/21
$$\:\mathrm{I}\:\mathrm{guess}\:\mathrm{the}\:\mathrm{question}\:\mathrm{area}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{formed} \\ $$$$\mathrm{by}\:\mathrm{x}−\mathrm{axis}\:,\:\mathrm{tangent}\:\mathrm{and}\:\mathrm{normal}\:\mathrm{line} \\ $$$$\mathrm{tangent}\:\mathrm{line}\::\:\mathrm{3x}+\mathrm{4y}=\mathrm{43}\:\Rightarrow\:\mathrm{intersect}\:\mathrm{the} \\ $$$$\mathrm{x}−\mathrm{axis}\:\mathrm{at}\:\mathrm{G}\left(\frac{\mathrm{43}}{\mathrm{3}}\:,\mathrm{0}\:\right) \\ $$$$\mathrm{normal}\:\mathrm{line}\::\:\mathrm{4x}−\mathrm{3y}=−\mathrm{1}\:\Rightarrow\mathrm{intersect}\:\mathrm{the} \\ $$$$\mathrm{x}−\mathrm{axis}\:\mathrm{at}\:\mathrm{P}\left(−\frac{\mathrm{1}}{\mathrm{4}},\mathrm{0}\right)\:\mathrm{and}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{y}−\mathrm{axis} \\ $$$$\mathrm{at}\:\mathrm{R}\left(\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{3}}\right)\:. \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{7}.\left(\frac{\mathrm{43}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\mathrm{A}=\:\frac{\mathrm{7}}{\mathrm{2}}.\left(\frac{\mathrm{175}}{\mathrm{12}}\right)=\:\frac{\mathrm{1125}}{\mathrm{24}}.\:\mathrm{Therefore} \\ $$$$\mathrm{24A}\:=\:\mathrm{1125} \\ $$