Question Number 75950 by turbo msup by abdo last updated on 21/Dec/19
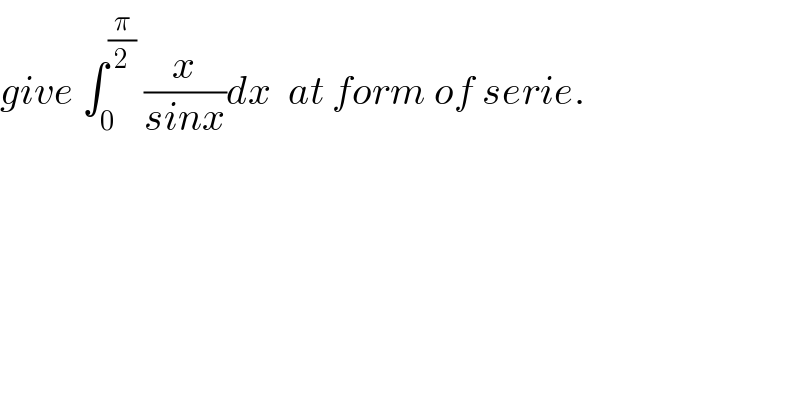
$${give}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx}\:\:{at}\:{form}\:{of}\:{serie}. \\ $$
Commented by mathmax by abdo last updated on 22/Dec/19
![let A = ∫_0 ^(π/2) (x/(sinx))dx changement tan((x/2))=t give A =2∫_0 ^1 ((arctan(t))/((2t)/(1+t^2 )))((2dt)/(1+t^2 )) =2 ∫_0 ^1 ((arctan(t))/t)dt we have (d/dt)(arctant) =(1/(1+t^2 )) =Σ_(n=0) ^∞ (−1)^n t^(2n) ⇒ arctan(t) =Σ_(n=0) ^∞ (−1)^n (t^(2n+1) /(2n+1)) +c (c=0) ⇒ ((arctan(t))/t) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))t^(2n) ⇒∫_0 ^1 ((arctan(t))/t)dt=Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))∫_0 ^1 t^(2n) dt =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)))[(1/(2n+1))t^(2n+1) ]_0 ^1 =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ⇒ A =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 ))](https://www.tinkutara.com/question/Q76046.png)
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{x}}{{sinx}}{dx}\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left({t}\right)}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctan}\left({t}\right)}{{t}}{dt}\:\:{we}\:{have} \\ $$$$\frac{{d}}{{dt}}\left({arctant}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$${arctan}\left({t}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:+{c}\:\:\:\:\left({c}=\mathrm{0}\right)\:\Rightarrow \\ $$$$\frac{{arctan}\left({t}\right)}{{t}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}} \:\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctan}\left({t}\right)}{{t}}{dt}=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}{n}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)}\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 22/Dec/19
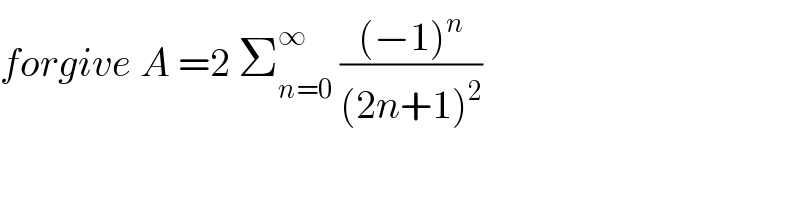
$${forgive}\:{A}\:=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
