Question Number 133231 by SOMEDAVONG last updated on 20/Feb/21
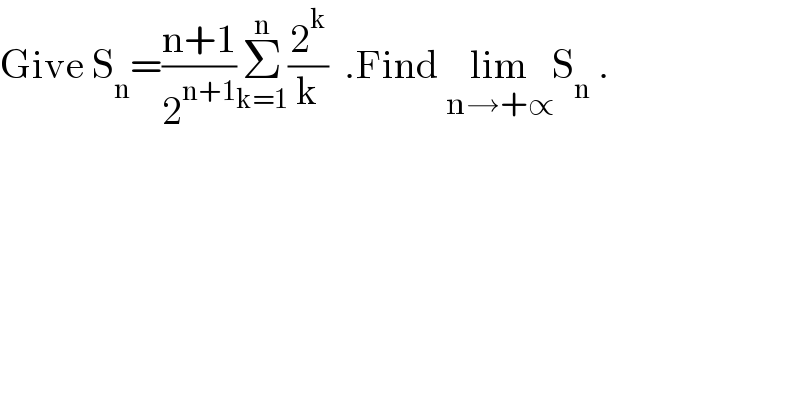
$$\mathrm{Give}\:\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{2}^{\mathrm{k}} }{\mathrm{k}}\:\:.\mathrm{Find}\:\underset{\mathrm{n}\rightarrow+\propto} {\mathrm{lim}S}_{\mathrm{n}} \:. \\ $$
Answered by Ar Brandon last updated on 21/Feb/21
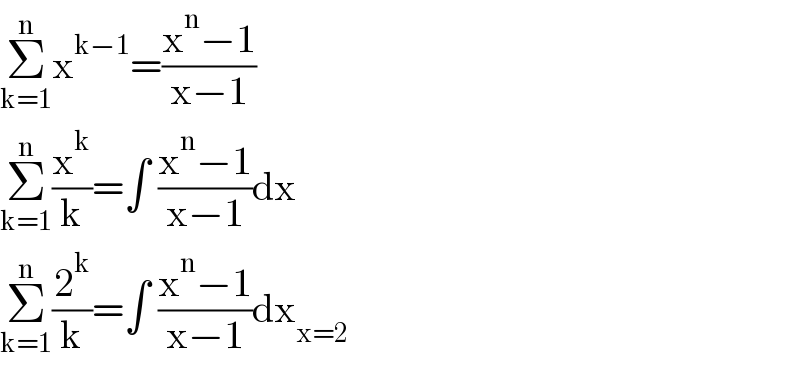
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}^{\mathrm{k}−\mathrm{1}} =\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{x}^{\mathrm{k}} }{\mathrm{k}}=\int\:\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mathrm{dx} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{2}^{\mathrm{k}} }{\mathrm{k}}=\int\:\frac{\mathrm{x}^{\mathrm{n}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}_{\mathrm{x}=\mathrm{2}} \\ $$
