Menu Close

give-the-equation-of-tangente-at-p-x-0-f-x-0-1-f-x-e-x-2-ln-1-2x-x-0-1-2-f-x-x-2-3-arctan-x-2-x-0-1-3-f-x-e-x-sin-pix-x-2-3-x-0-1-2-4-f-x-e-x-e-x-2-

Tinku Tara 0 Comments
Pin




Question Number 78136 by msup trace by abdo last updated on 14/Jan/20
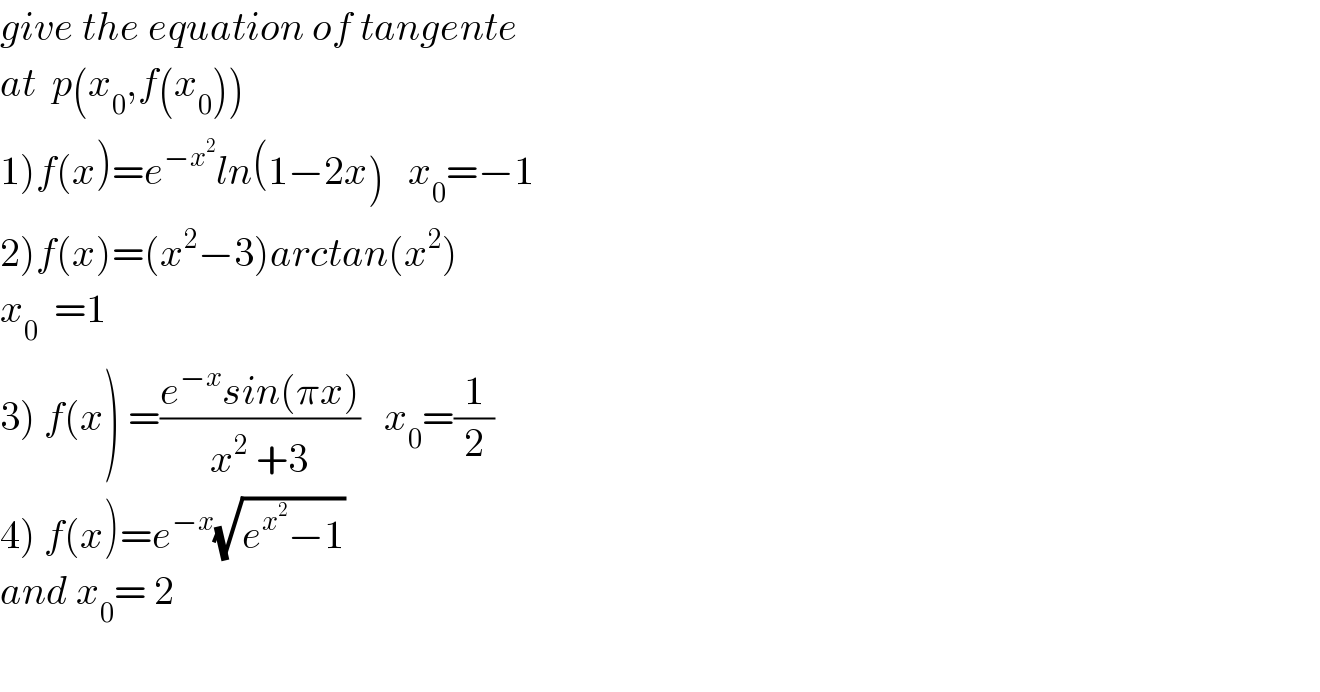
give the equation of tangente at p(x_0 ,f(x_0 )) 1)f(x)=e^(−x^2 ) ln(1−2x) x_0 =−1 2)f(x)=(x^2 −3)arctan(x^2 ) x_0 =1 3) f(x) =((e^(−x) sin(πx))/(x^2 +3)) x_0 =(1/2) 4) f(x)=e^(−x) (√(e^x^2 −1)) and x_0 = 2
$${give}\:{the}\:{equation}\:{of}\:{tangente} \\ $$$${at}\:\:{p}\left({x}_{\mathrm{0}} ,{f}\left({x}_{\mathrm{0}} \right)\right) \\ $$$$\left.\mathrm{1}\right){f}\left({x}\right)={e}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{1}−\mathrm{2}{x}\right)\:\:\:{x}_{\mathrm{0}} =−\mathrm{1} \\ $$$$\left.\mathrm{2}\right){f}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{3}\right){arctan}\left({x}^{\mathrm{2}} \right) \\ $$$${x}_{\mathrm{0}} \:\:=\mathrm{1} \\ $$$$\left.\mathrm{3}\right)\:{f}\left({x}\right)\:=\frac{{e}^{−{x}} {sin}\left(\pi{x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{3}}\:\:\:{x}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{4}\right)\:{f}\left({x}\right)={e}^{−{x}} \sqrt{{e}^{{x}^{\mathrm{2}} } −\mathrm{1}} \\ $$$${and}\:{x}_{\mathrm{0}} =\:\mathrm{2} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 14/Jan/20
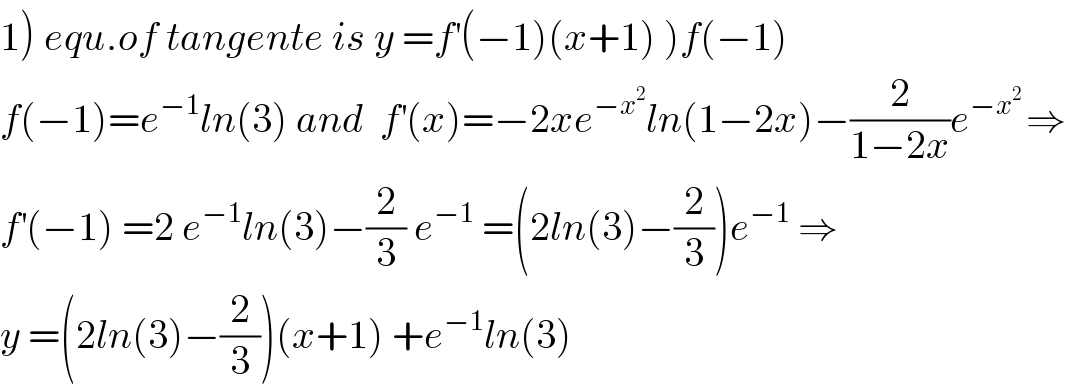
1) equ.of tangente is y =f^′ (−1)(x+1) )f(−1) f(−1)=e^(−1) ln(3) and f^′ (x)=−2xe^(−x^2 ) ln(1−2x)−(2/(1−2x))e^(−x^2 ) ⇒ f^′ (−1) =2 e^(−1) ln(3)−(2/3) e^(−1) =(2ln(3)−(2/3))e^(−1) ⇒ y =(2ln(3)−(2/3))(x+1) +e^(−1) ln(3)
$$\left.\mathrm{1}\left.\right)\:{equ}.{of}\:{tangente}\:{is}\:{y}\:={f}^{'} \left(−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\:\right){f}\left(−\mathrm{1}\right) \\ $$$${f}\left(−\mathrm{1}\right)={e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right)\:{and}\:\:{f}^{'} \left({x}\right)=−\mathrm{2}{xe}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{1}−\mathrm{2}{x}\right)−\frac{\mathrm{2}}{\mathrm{1}−\mathrm{2}{x}}{e}^{−{x}^{\mathrm{2}} \:} \Rightarrow \\ $$$${f}^{'} \left(−\mathrm{1}\right)\:=\mathrm{2}\:{e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\:{e}^{−\mathrm{1}} \:=\left(\mathrm{2}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\right){e}^{−\mathrm{1}} \:\Rightarrow \\ $$$${y}\:=\left(\mathrm{2}{ln}\left(\mathrm{3}\right)−\frac{\mathrm{2}}{\mathrm{3}}\right)\left({x}+\mathrm{1}\right)\:+{e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right) \\ $$
Commented by mathmax by abdo last updated on 14/Jan/20
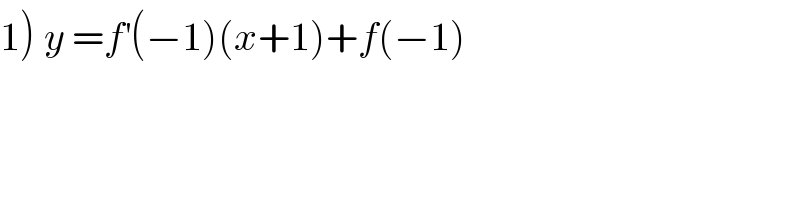
1) y =f^′ (−1)(x+1)+f(−1)
$$\left.\mathrm{1}\right)\:{y}\:={f}^{'} \left(−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+{f}\left(−\mathrm{1}\right) \\ $$
Commented by jagoll last updated on 14/Jan/20
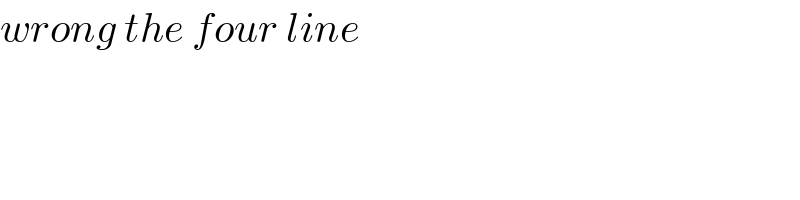
wrong the four line
$${wrong}\:{the}\:{four}\:{line}\: \\ $$
Commented by msup trace by abdo last updated on 15/Jan/20
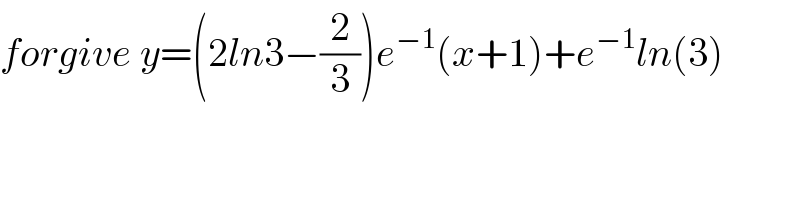
forgive y=(2ln3−(2/3))e^(−1) (x+1)+e^(−1) ln(3)
$${forgive}\:{y}=\left(\mathrm{2}{ln}\mathrm{3}−\frac{\mathrm{2}}{\mathrm{3}}\right){e}^{−\mathrm{1}} \left({x}+\mathrm{1}\right)+{e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right) \\ $$
Commented by msup trace by abdo last updated on 15/Jan/20
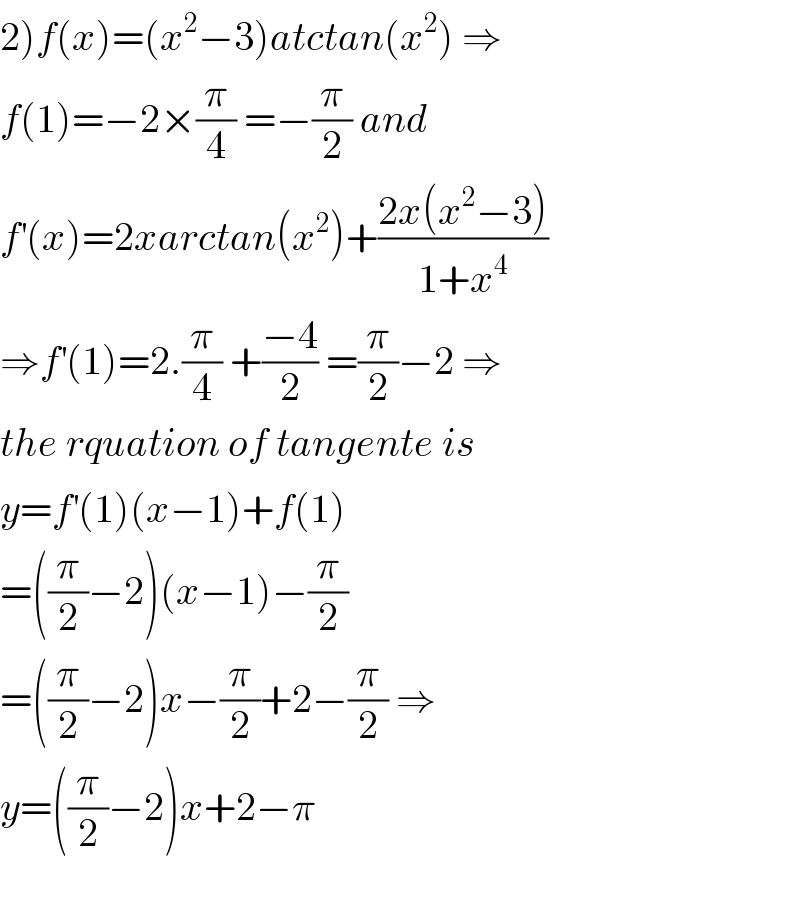
2)f(x)=(x^2 −3)atctan(x^2 ) ⇒ f(1)=−2×(π/4) =−(π/2) and f^′ (x)=2xarctan(x^2 )+((2x(x^2 −3))/(1+x^4 )) ⇒f^′ (1)=2.(π/4) +((−4)/2) =(π/2)−2 ⇒ the rquation of tangente is y=f^′ (1)(x−1)+f(1) =((π/2)−2)(x−1)−(π/2) =((π/2)−2)x−(π/2)+2−(π/2) ⇒ y=((π/2)−2)x+2−π
$$\left.\mathrm{2}\right){f}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{3}\right){atctan}\left({x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{2}×\frac{\pi}{\mathrm{4}}\:=−\frac{\pi}{\mathrm{2}}\:{and} \\ $$$${f}^{'} \left({x}\right)=\mathrm{2}{xarctan}\left({x}^{\mathrm{2}} \right)+\frac{\mathrm{2}{x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$$$\Rightarrow{f}^{'} \left(\mathrm{1}\right)=\mathrm{2}.\frac{\pi}{\mathrm{4}}\:+\frac{−\mathrm{4}}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}}−\mathrm{2}\:\Rightarrow \\ $$$${the}\:{rquation}\:{of}\:{tangente}\:{is} \\ $$$${y}={f}^{'} \left(\mathrm{1}\right)\left({x}−\mathrm{1}\right)+{f}\left(\mathrm{1}\right) \\ $$$$=\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)−\frac{\pi}{\mathrm{2}} \\ $$$$=\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\right){x}−\frac{\pi}{\mathrm{2}}+\mathrm{2}−\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${y}=\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}\right){x}+\mathrm{2}−\pi \\ $$$$ \\ $$
Answered by jagoll last updated on 14/Jan/20
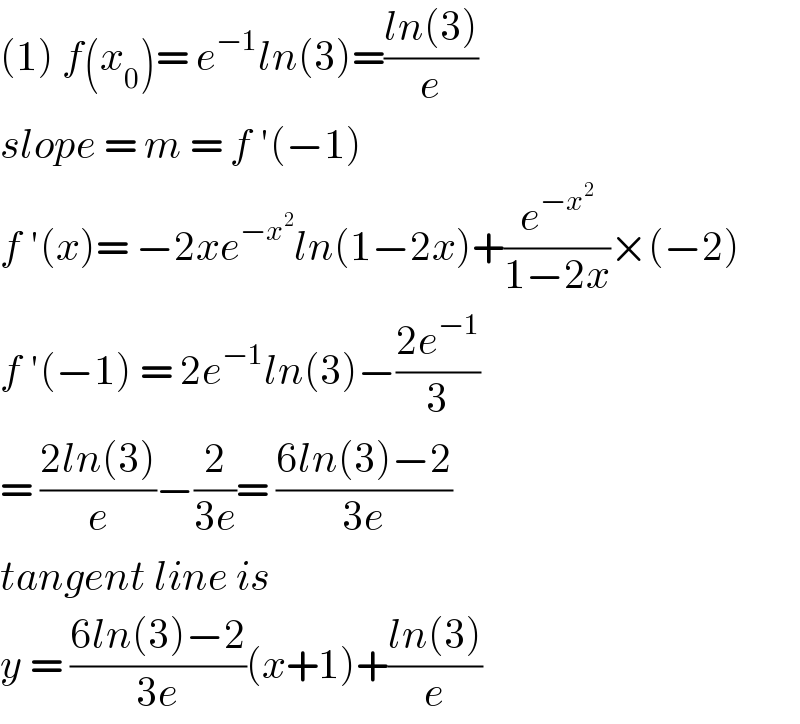
(1) f(x_0 )= e^(−1) ln(3)=((ln(3))/e) slope = m = f ′(−1) f ′(x)= −2xe^(−x^2 ) ln(1−2x)+(e^(−x^2 ) /(1−2x))×(−2) f ′(−1) = 2e^(−1) ln(3)−((2e^(−1) )/3) = ((2ln(3))/e)−(2/(3e))= ((6ln(3)−2)/(3e)) tangent line is y = ((6ln(3)−2)/(3e))(x+1)+((ln(3))/e)
$$\left(\mathrm{1}\right)\:{f}\left({x}_{\mathrm{0}} \right)=\:{e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right)=\frac{{ln}\left(\mathrm{3}\right)}{{e}} \\ $$$${slope}\:=\:{m}\:=\:{f}\:'\left(−\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)=\:−\mathrm{2}{xe}^{−{x}^{\mathrm{2}} } {ln}\left(\mathrm{1}−\mathrm{2}{x}\right)+\frac{{e}^{−{x}^{\mathrm{2}} } }{\mathrm{1}−\mathrm{2}{x}}×\left(−\mathrm{2}\right) \\ $$$${f}\:'\left(−\mathrm{1}\right)\:=\:\mathrm{2}{e}^{−\mathrm{1}} {ln}\left(\mathrm{3}\right)−\frac{\mathrm{2}{e}^{−\mathrm{1}} }{\mathrm{3}} \\ $$$$=\:\frac{\mathrm{2}{ln}\left(\mathrm{3}\right)}{{e}}−\frac{\mathrm{2}}{\mathrm{3}{e}}=\:\frac{\mathrm{6}{ln}\left(\mathrm{3}\right)−\mathrm{2}}{\mathrm{3}{e}} \\ $$$${tangent}\:{line}\:{is}\: \\ $$$${y}\:=\:\frac{\mathrm{6}{ln}\left(\mathrm{3}\right)−\mathrm{2}}{\mathrm{3}{e}}\left({x}+\mathrm{1}\right)+\frac{{ln}\left(\mathrm{3}\right)}{{e}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *