Question Number 75509 by ~blr237~ last updated on 12/Dec/19
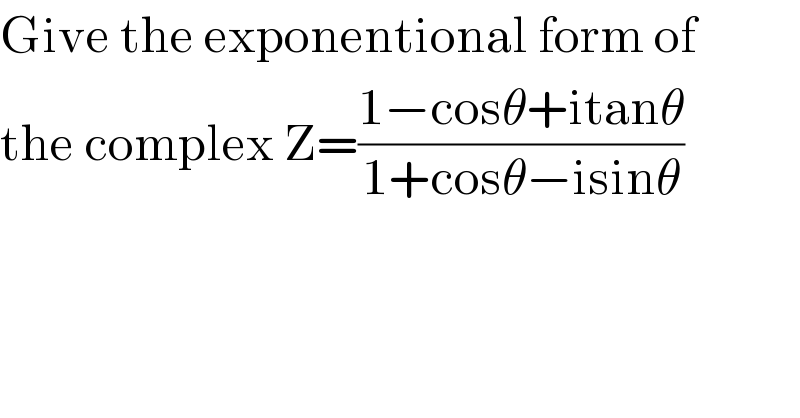
$$\mathrm{Give}\:\mathrm{the}\:\mathrm{exponentional}\:\mathrm{form}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{complex}\:\mathrm{Z}=\frac{\mathrm{1}−\mathrm{cos}\theta+\mathrm{itan}\theta}{\mathrm{1}+\mathrm{cos}\theta−\mathrm{isin}\theta} \\ $$
Answered by MJS last updated on 12/Dec/19
![((1−c+it)/(1+c−is))=((c^2 −2c−st+1)/(c^2 −2c+s^2 +1))−((cs+ct−s−t)/(c^2 −2c+s^2 +1))i= [c^2 +s^2 =1] =((c^2 −2c−st+1)/(2−2c))−(((c−1)(s+t))/(2−2c))i= =((c^2 −2c−st+1)/(2−2c))+((s+t)/2)i= [t=(s/c)] =−((c^3 −2c^2 +c−s^2 )/(2c(c−1)))+(((c+1)s)/(2c))i= [s^2 =1−c^2 ] =−((c^2 +1)/(2c))+(((c+1)s)/(2c))i abs (−((c^2 +1)/(2c))+(((c+1)s)/(2c))i) = [again using s^2 =1−c^2 ] =((√(1+c+c^2 −c^3 ))/( (√2)∣c∣)) arg (−((c^2 +1)/(2c))+(((c+1)s)/(2c))i) = −arctan (((c+1)s)/(c^2 +1)) ⇒ Z=e^(−i arctan (((1+cos θ)sin θ)/(1+cos^2 θ))) ((√(1+cos θ+ cos^2 θ −cos^3 θ))/( (√2)∣cos θ∣))](https://www.tinkutara.com/question/Q75529.png)
$$\frac{\mathrm{1}−{c}+\mathrm{i}{t}}{\mathrm{1}+{c}−\mathrm{i}{s}}=\frac{{c}^{\mathrm{2}} −\mathrm{2}{c}−{st}+\mathrm{1}}{{c}^{\mathrm{2}} −\mathrm{2}{c}+{s}^{\mathrm{2}} +\mathrm{1}}−\frac{{cs}+{ct}−{s}−{t}}{{c}^{\mathrm{2}} −\mathrm{2}{c}+{s}^{\mathrm{2}} +\mathrm{1}}\mathrm{i}= \\ $$$$\:\:\:\:\:\left[{c}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{1}\right] \\ $$$$=\frac{{c}^{\mathrm{2}} −\mathrm{2}{c}−{st}+\mathrm{1}}{\mathrm{2}−\mathrm{2}{c}}−\frac{\left({c}−\mathrm{1}\right)\left({s}+{t}\right)}{\mathrm{2}−\mathrm{2}{c}}\mathrm{i}= \\ $$$$=\frac{{c}^{\mathrm{2}} −\mathrm{2}{c}−{st}+\mathrm{1}}{\mathrm{2}−\mathrm{2}{c}}+\frac{{s}+{t}}{\mathrm{2}}\mathrm{i}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{s}}{{c}}\right] \\ $$$$=−\frac{{c}^{\mathrm{3}} −\mathrm{2}{c}^{\mathrm{2}} +{c}−{s}^{\mathrm{2}} }{\mathrm{2}{c}\left({c}−\mathrm{1}\right)}+\frac{\left({c}+\mathrm{1}\right){s}}{\mathrm{2}{c}}\mathrm{i}= \\ $$$$\:\:\:\:\:\left[{s}^{\mathrm{2}} =\mathrm{1}−{c}^{\mathrm{2}} \right] \\ $$$$=−\frac{{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{c}}+\frac{\left({c}+\mathrm{1}\right){s}}{\mathrm{2}{c}}\mathrm{i} \\ $$$$\mathrm{abs}\:\left(−\frac{{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{c}}+\frac{\left({c}+\mathrm{1}\right){s}}{\mathrm{2}{c}}\mathrm{i}\right)\:= \\ $$$$\:\:\:\:\:\left[\mathrm{again}\:\mathrm{using}\:{s}^{\mathrm{2}} =\mathrm{1}−{c}^{\mathrm{2}} \right] \\ $$$$=\frac{\sqrt{\mathrm{1}+{c}+{c}^{\mathrm{2}} −{c}^{\mathrm{3}} }}{\:\sqrt{\mathrm{2}}\mid{c}\mid} \\ $$$$\mathrm{arg}\:\left(−\frac{{c}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{c}}+\frac{\left({c}+\mathrm{1}\right){s}}{\mathrm{2}{c}}\mathrm{i}\right)\:= \\ $$$$−\mathrm{arctan}\:\frac{\left({c}+\mathrm{1}\right){s}}{{c}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${Z}=\mathrm{e}^{−\mathrm{i}\:\mathrm{arctan}\:\frac{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta}} \frac{\sqrt{\mathrm{1}+\mathrm{cos}\:\theta+\:\mathrm{cos}^{\mathrm{2}} \:\theta\:−\mathrm{cos}^{\mathrm{3}} \:\theta}}{\:\sqrt{\mathrm{2}}\mid\mathrm{cos}\:\theta\mid} \\ $$
